Casson handle
A certain kind of smooth manifold pair 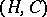 that, by a foundational theorem of M. Freedman [a3], is homeomorphic to a
that, by a foundational theorem of M. Freedman [a3], is homeomorphic to a  -dimensional open
-dimensional open  -handle
-handle 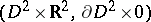 (cf. Handle theory). Casson handles are the key to understanding topological
(cf. Handle theory). Casson handles are the key to understanding topological  -manifolds [a4]. The fundamental theorems of high-dimensional manifold topology (cf. Topology of manifolds), namely the surgery and
-manifolds [a4]. The fundamental theorems of high-dimensional manifold topology (cf. Topology of manifolds), namely the surgery and  -cobordism theorems, fail for smooth
-cobordism theorems, fail for smooth 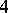 -manifolds because they depend on finding an embedded
-manifolds because they depend on finding an embedded  -dimensional disc
-dimensional disc  in a given manifold
in a given manifold  , with specified boundary
, with specified boundary 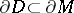 . In dimensions
. In dimensions 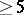 , such an embedding is easily constructed by general position, but in dimension
, such an embedding is easily constructed by general position, but in dimension 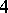 , immersed surfaces cannot be made embedded by perturbation (cf. Immersion of a manifold; Immersion). By work of A. Casson [a2], it is often possible to embed a Casson handle in the required
, immersed surfaces cannot be made embedded by perturbation (cf. Immersion of a manifold; Immersion). By work of A. Casson [a2], it is often possible to embed a Casson handle in the required  -manifold, with
-manifold, with 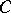 mapping to the required circle, so Freedman's theorem provides a homeomorphically embedded disc. This leads to proofs of the above fundamental theorems for topological
mapping to the required circle, so Freedman's theorem provides a homeomorphically embedded disc. This leads to proofs of the above fundamental theorems for topological  -manifolds (that is, manifolds without specified smooth structures), provided that the fundamental groups involved are not too "large" . In particular, Freedman obtained a complete classification of closed simply-connected topological
-manifolds (that is, manifolds without specified smooth structures), provided that the fundamental groups involved are not too "large" . In particular, Freedman obtained a complete classification of closed simply-connected topological 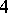 -manifolds in terms of the intersection pairing (cf. also Intersection theory).
-manifolds in terms of the intersection pairing (cf. also Intersection theory).
A Casson handle is constructed as a union of kinky handles. A kinky handle 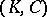 can be defined as the smooth, oriented
can be defined as the smooth, oriented  -manifold
-manifold 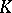 arising as a closed regular neighbourhood of a generically immersed (but not embedded)
arising as a closed regular neighbourhood of a generically immersed (but not embedded)  -disc
-disc 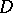 in an oriented
in an oriented 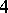 -manifold, together with the boundary circle
-manifold, together with the boundary circle 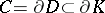 . For each pair
. For each pair  of non-negative integers, not both
of non-negative integers, not both  , there is a unique oriented diffeomorphism type of kinky handle, corresponding to a disc
, there is a unique oriented diffeomorphism type of kinky handle, corresponding to a disc 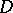 with
with 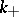 positive and
positive and  negative self-intersections. The attaching circle
negative self-intersections. The attaching circle 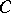 has a canonical framing of its normal bundle in
has a canonical framing of its normal bundle in  , obtained by restricting any normal framing of an embedded, compact, oriented surface
, obtained by restricting any normal framing of an embedded, compact, oriented surface  . Equivalently, the framing is obtained from the normal framing of
. Equivalently, the framing is obtained from the normal framing of  by adding
by adding  right twists (relative to the boundary orientation on
right twists (relative to the boundary orientation on 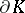 ). There is also a canonical (up to diffeomorphism) embedded collection of normally framed circles
). There is also a canonical (up to diffeomorphism) embedded collection of normally framed circles  in
in  , with the property that attaching
, with the property that attaching  -handles
-handles 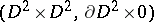 to
to 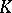 along these circles (identifying
along these circles (identifying 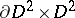 with a neighbourhood of
with a neighbourhood of 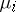 so that the framings correspond) transforms
so that the framings correspond) transforms 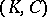 into a standard
into a standard  -handle.
-handle.
An  -stage Casson tower
-stage Casson tower 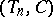 is defined inductively, as follows: A
is defined inductively, as follows: A 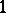 -stage tower is a kinky handle
-stage tower is a kinky handle  with canonical circles
with canonical circles 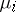 , and for
, and for 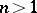 an
an  -stage tower
-stage tower  is obtained from an
is obtained from an 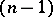 -stage tower
-stage tower 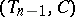 by attaching a kinky handle
by attaching a kinky handle 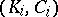 to each of the canonical circles
to each of the canonical circles  of
of 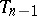 , identifying tubular neighbourhoods (cf. Tubular neighbourhood) of
, identifying tubular neighbourhoods (cf. Tubular neighbourhood) of  and
and  so as to match the canonical framings. The canonical framed circles of
so as to match the canonical framings. The canonical framed circles of 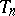 are those of the newly attached kinky handles. If one continues this construction to form an infinite sequence
are those of the newly attached kinky handles. If one continues this construction to form an infinite sequence  , the interior of the resulting manifold
, the interior of the resulting manifold
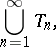 |
together with a tubular neighbourhood of the attaching circle 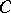 of
of 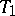 , is a Casson handle
, is a Casson handle  . According to Freedman,
. According to Freedman,  is homeomorphic to
is homeomorphic to 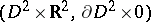 with the canonical framing on
with the canonical framing on  corresponding to the product framing on
corresponding to the product framing on 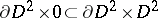 . A newer, more powerful version of the theory [a4] relies on generalized Casson handles that have occasionally been called Freedman handles. These have most layers of kinky handles replaced by manifolds
. A newer, more powerful version of the theory [a4] relies on generalized Casson handles that have occasionally been called Freedman handles. These have most layers of kinky handles replaced by manifolds 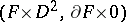 for
for 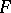 a compact, oriented surface with boundary a circle.
a compact, oriented surface with boundary a circle.
Although all Casson handles are homeomorphic, gauge theory shows that the differential topology is much more complex. There are uncountably many diffeomorphism types of Casson handles [a6]. Casson handles are indexed by based trees without any finite branches, with signs attached to the edges. Each vertex represents a kinky handle (with the base point representing  ) and each edge represents a self-intersection. It is not presently known whether different signed trees can correspond to diffeomorphic Casson handles. While it is also not known if there is any Casson handle
) and each edge represents a self-intersection. It is not presently known whether different signed trees can correspond to diffeomorphic Casson handles. While it is also not known if there is any Casson handle 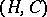 that admits a smoothly embedded disc bounded by
that admits a smoothly embedded disc bounded by  , such a disc cannot exist if the corresponding tree has an infinite branch (from the base point) for which all signs are the same [a1], [a7]. For any non-negative integers
, such a disc cannot exist if the corresponding tree has an infinite branch (from the base point) for which all signs are the same [a1], [a7]. For any non-negative integers 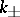 , not both
, not both  , there is a Casson handle with
, there is a Casson handle with  having exactly
having exactly 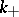 positive and
positive and  negative self-intersections, such that any generically immersed smooth disc in
negative self-intersections, such that any generically immersed smooth disc in 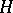 bounded by
bounded by 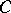 also has at least
also has at least 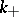 positive and
positive and 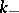 negative intersections [a5].
negative intersections [a5].
References
| [a1] | Ž. Bižaca, "An explicit family of exotic Casson handles" Proc. Amer. Math. Soc. , 123 (1995) pp. 1297–1302 |
| [a2] | A. Casson, "Three lectures on new infinite constructions in  -dimensional manifolds" , A la Recherche de la Topologie Perdue , Progress in Mathematics , 62 , Birkhäuser (1986) pp. 201–244 (notes prepared by L. Guillou) -dimensional manifolds" , A la Recherche de la Topologie Perdue , Progress in Mathematics , 62 , Birkhäuser (1986) pp. 201–244 (notes prepared by L. Guillou) |
| [a3] | M. Freedman, "The topology of four-dimensional manifolds" J. Diff. Geom. , 17 (1982) pp. 357–453 |
| [a4] | M. Freedman, F. Quinn, "Topology of 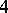 -manifolds" , Princeton Math. Ser. , 39 , Princeton Univ. Press (1990) -manifolds" , Princeton Math. Ser. , 39 , Princeton Univ. Press (1990) |
| [a5] | R. Gompf, "Infinite families of Casson handles and topological disks" Topology , 23 (1984) pp. 395–400 |
| [a6] | R. Gompf, "Periodic ends and knot concordance" Topology Appl. , 32 (1989) pp. 141–148 |
| [a7] | L. Rudolph, "Quasipositivity as an obstruction to sliceness" Bull. Amer. Math. Soc. , 29 (1993) pp. 51–59 |
Casson handle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Casson_handle&oldid=11328