Cartesian orthogonal coordinate system
orthonormal
A rectilinear system of coordinates in a Euclidean space.
On a plane, a Cartesian rectangular coordinate system is defined by two mutually-perpendicular lines, the coordinate axes, on each of which a positive direction has been chosen and a segment of unit length has been specified. The point of intersection ( ) of the coordinate axes is said to be the coordinate origin. One of the coordinate axes
) of the coordinate axes is said to be the coordinate origin. One of the coordinate axes 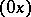 is said to be the abscissa axis; the other one (
is said to be the abscissa axis; the other one (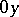 ) is said to be the ordinate axis. The coordinate axes subdivide the plane into four equal regions, called quarters or quadrants.
) is said to be the ordinate axis. The coordinate axes subdivide the plane into four equal regions, called quarters or quadrants.
The rectangular Cartesian coordinates of a point 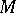 are represented by an ordered pair of numbers
are represented by an ordered pair of numbers 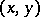 , the first of which (the abscissa) is equal to the magnitude of the orthogonal projection of the directed segment
, the first of which (the abscissa) is equal to the magnitude of the orthogonal projection of the directed segment 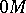 on the abscissa axis, the second one (the ordinate) being the orthogonal projection of the directed segment
on the abscissa axis, the second one (the ordinate) being the orthogonal projection of the directed segment  on the ordinate axis.
on the ordinate axis.
A Cartesian rectangular coordinate system in a three-dimensional space is defined similarly to the case of the plane: by an abscissa axis, by an ordinate axis, by an applicate axis, and by a coordinate origin  . The plane passing through the coordinate axes are said to be the coordinate planes. They subdivide the space into eight regions, the octants.
. The plane passing through the coordinate axes are said to be the coordinate planes. They subdivide the space into eight regions, the octants.
A skew-angled (general) Cartesian coordinate system is also occasionally used. As distinct from the rectangular system, the angles between the coordinate axes need not be straight angles.
Named in this way after R. Descartes [1], who introduced the method of rectilinear coordinates.
References
| [1] | R. Descartes, "Geometria" , Leiden (1649) |
Cartesian orthogonal coordinate system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartesian_orthogonal_coordinate_system&oldid=18006