Cartan theorem
Cartan's theorem on the highest weight vector. Let 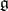 be a complex semi-simple Lie algebra, let
be a complex semi-simple Lie algebra, let 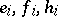 ,
, 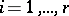 , be canonical generators of it, that is, linearly-independent generators for which the following relations hold:
, be canonical generators of it, that is, linearly-independent generators for which the following relations hold:
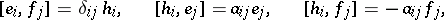 |
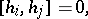 |
where 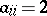 ,
, 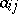 are non-positive integers when
are non-positive integers when 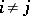 ,
, 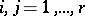 ,
, 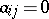 implies
implies 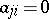 , and let
, and let 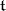 be the Cartan subalgebra of
be the Cartan subalgebra of 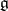 which is the linear span of
which is the linear span of 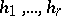 . Also let
. Also let 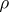 be a linear representation of
be a linear representation of 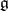 in a complex finite-dimensional space
in a complex finite-dimensional space 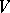 . Then there exists a non-zero vector
. Then there exists a non-zero vector  for which
for which
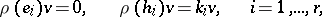 |
where the 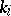 are certain numbers. This theorem was established by E. Cartan [1]. The vector
are certain numbers. This theorem was established by E. Cartan [1]. The vector  is called the highest weight vector of the representation
is called the highest weight vector of the representation 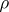 and the linear function
and the linear function 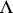 on
on 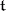 defined by the condition
defined by the condition 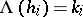 ,
, 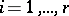 , is called the highest weight of the representation
, is called the highest weight of the representation 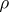 corresponding to
corresponding to  . The ordered set
. The ordered set 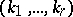 is called the set of numerical marks of the highest weight
is called the set of numerical marks of the highest weight 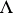 . Cartan's theorem gives a complete classification of irreducible finite-dimensional linear representations of a complex semi-simple finite-dimensional Lie algebra. It asserts that each finite-dimensional complex irreducible representation of
. Cartan's theorem gives a complete classification of irreducible finite-dimensional linear representations of a complex semi-simple finite-dimensional Lie algebra. It asserts that each finite-dimensional complex irreducible representation of 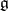 has a unique highest weight vector (up to proportionality), and that the numerical marks of the corresponding highest weight are non-negative integers. Two finite-dimensional irreducible representations are equivalent if and only if the corresponding highest weights are the same. Any set of non-negative integers is the set of numerical marks of the highest weight of some finite-dimensional complex irreducible representation.
has a unique highest weight vector (up to proportionality), and that the numerical marks of the corresponding highest weight are non-negative integers. Two finite-dimensional irreducible representations are equivalent if and only if the corresponding highest weights are the same. Any set of non-negative integers is the set of numerical marks of the highest weight of some finite-dimensional complex irreducible representation.
References
| [1] | E. Cartan, "Les tenseurs irréductibles et les groupes linéaires simples et semi-simples" Bull. Sci. Math. , 49 (1925) pp. 130–152 |
| [2] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) |
| [3] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Ecole Norm. Sup. (1955) |
| [4] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [5] | J. Dixmier, "Enveloping algebras" , North-Holland (1977) (Translated from French) |
| [6] | A. Borel (ed.) R. Carter (ed.) C.W. Curtis (ed.) N. Iwahori (ed.) T.A. Springer (ed.) R. Steinberg (ed.) , Seminar on algebraic groups and related finite groups , Lect. notes in math. , 131 , Springer (1970) |
Comments
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) |
Cartan's theorem in the theory of functions of several complex variables. These are the so-called theorems A and B on coherent analytic sheaves on Stein manifolds, first proved by H. Cartan [1]. Let 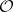 be the sheaf of germs of holomorphic functions on a complex manifold
be the sheaf of germs of holomorphic functions on a complex manifold 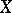 . A sheaf
. A sheaf 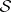 of
of 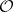 -modules on
-modules on 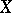 is called a coherent analytic sheaf if there exists in a neighbourhood of each point
is called a coherent analytic sheaf if there exists in a neighbourhood of each point 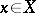 an exact sequence of sheaves
an exact sequence of sheaves
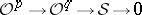 |
for some natural numbers 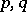 . Examples are all locally finitely-generated subsheaves of
. Examples are all locally finitely-generated subsheaves of 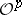 .
.
Theorem A. Let 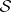 be a coherent analytic sheaf on a Stein manifold
be a coherent analytic sheaf on a Stein manifold 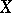 . Then there exists for each point
. Then there exists for each point 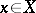 a finite number of global sections
a finite number of global sections 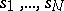 of
of 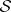 such that any element
such that any element  of the fibre
of the fibre 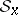 is representable in the form
is representable in the form
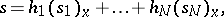 |
with all 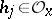 . (In other words, locally
. (In other words, locally 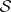 is finitely generated over
is finitely generated over 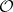 by its global sections.)
by its global sections.)
Theorem B. Let 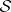 be a coherent analytic sheaf on a Stein manifold
be a coherent analytic sheaf on a Stein manifold 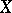 . Then all cohomology groups of
. Then all cohomology groups of 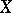 of order
of order 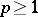 with coefficients in
with coefficients in 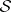 are trivial:
are trivial:
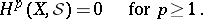 |
These Cartan theorems have many applications. From Theorem A, various theorems can be obtained on the existence of global analytic objects on Stein manifolds. The main corollary of Theorem B is the solvability of the 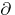 -problem: On a Stein manifold, the equation
-problem: On a Stein manifold, the equation 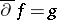 with the compatibility condition
with the compatibility condition 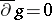 is always solvable.
is always solvable.
The scheme of application of Theorem B is as follows: If
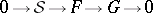 |
is an exact sequence of sheaves on 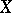 , then the sequence
, then the sequence
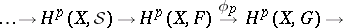 |
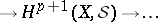 |
is also exact. If 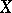 is a Stein manifold, then
is a Stein manifold, then
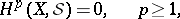 |
and hence, 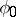 is mapping onto and the
is mapping onto and the 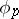 ,
, 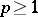 , are isomorphisms.
, are isomorphisms.
Theorem B is best possible: If on a complex manifold 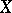 the group
the group 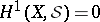 for every coherent analytic sheaf
for every coherent analytic sheaf 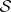 , then
, then 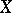 is a Stein manifold. Theorems A and B together with their numerous corollaries constitute the so-called Oka–Cartan theory of Stein manifolds. A corollary of these theorems is the solvability on Stein manifolds of all the classical problems of multi-dimensional complex analysis, such as the Cousin problem, the Levi problem, the Poincaré problem and others. Theorems A and B generalize verbatim to Stein spaces (cf. Stein space).
is a Stein manifold. Theorems A and B together with their numerous corollaries constitute the so-called Oka–Cartan theory of Stein manifolds. A corollary of these theorems is the solvability on Stein manifolds of all the classical problems of multi-dimensional complex analysis, such as the Cousin problem, the Levi problem, the Poincaré problem and others. Theorems A and B generalize verbatim to Stein spaces (cf. Stein space).
References
| [1] | H. Cartan, "Variétés analytiques complexes et cohomologie" R. Remmert (ed.) J.-P. Serre (ed.) , Collected works , Springer (1979) pp. 669–683 |
| [2] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [3] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) |
E.M. Chirka
Comments
In [a1] the theory related to Cartan's Theorems A and B is developed on the basis of integral representations, and not on the basis of sheaves, as in [2] or [a2], or on the basis of the Cauchy–Riemann equations, as in [3].
Generalizations to Stein manifolds are in [a2].
See also Cousin problems. For the Poincaré problem (on meromorphic functions), cf. Stein space and Meromorphic function.
References
| [a1] | G.M. [G.M. Khenkin] Henkin, J. Leiterer, "Theory of functions on complex manifolds" , Birkhäuser (1984) (Translated from Russian) |
| [a2] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1977) (Translated from German) |
| [a3] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) pp. Sect. 7.1 |
| [a4] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. VI, Par. 6 |
Cartan theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartan_theorem&oldid=15979