Cartan decomposition
A representation of a real non-compact semi-simple Lie algebra  (cf. Lie algebra, semi-simple) as a direct sum of vector spaces (*). If
(cf. Lie algebra, semi-simple) as a direct sum of vector spaces (*). If  denotes the complexification (complex envelope) of
denotes the complexification (complex envelope) of  (cf. Complexification of a Lie algebra), then there exists in
(cf. Complexification of a Lie algebra), then there exists in  a real compact subalgebra
a real compact subalgebra  of the same dimension as
of the same dimension as  such that the following decompositions into direct sums of vector spaces hold:
such that the following decompositions into direct sums of vector spaces hold:
 | (*) |
where 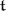 is the subalgebra of invariant elements of some involutory automorphism (involution)
is the subalgebra of invariant elements of some involutory automorphism (involution)  of
of  and
and 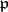 is the set of anti-invariant elements of
is the set of anti-invariant elements of 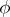 . The second formula is the Cartan decomposition of
. The second formula is the Cartan decomposition of  (see [1]). The Cartan decomposition reduces the classification of real non-compact semi-simple Lie algebras to that of compact semi-simple Lie algebras and involutory automorphisms in them.
(see [1]). The Cartan decomposition reduces the classification of real non-compact semi-simple Lie algebras to that of compact semi-simple Lie algebras and involutory automorphisms in them.
References
| [1] | S. Helgason, "Differential geometry and symmetric spaces" , Acad. Press (1962) |
Cartan decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartan_decomposition&oldid=17328