Carnot theorem

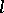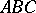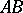A theorem on the product of the simple ratios in which the points of intersection of an algebraic curve with the sides of a triangle divide these sides. Suppose that the algebraic curve of order does not pass through any of the vertices of a triangle and intersects each side, extended if necessary, at points: the side at the points 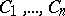; the side at the points ; and the side at the points . Then the product of the simple ratios

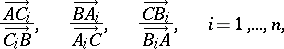is equal to 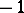if is odd, and 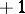if is even.

This statement is equivalent to the following: The product of the 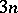ratios

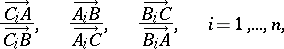is equal to .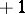

A special case of this theorem was proved by L. Carnot [1].

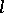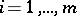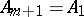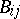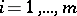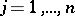If is a straight line then the Menelaus theorem is obtained. A generalization of Carnot's theorem is: Suppose that an algebraic curve of order intersects each of the straight lines , , , lying in the plane of this curve, at exactly points , ; . Then

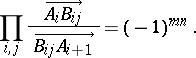References

[1]	L. Carnot, "Géométrie de position" , Paris (1803)