Carnap rule
rule of infinite induction, 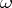 -rule
-rule
A derivation rule stating that if for an arithmetic formula 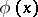 the propositions
the propositions 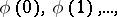 have been proved, then the proposition
have been proved, then the proposition 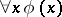 can be regarded as being proved. This rule was first brought into consideration by R. Carnap [1]. Carnap's rule uses an infinite set of premises and is therefore inadmissible within the structure of the formal theories of D. Hilbert. The concept of a derivation in a system with the Carnap rule is undecidable. In mathematical logic one uses, for the study of formal arithmetic, the constructive Carnap rule: If there is an algorithm which for a natural number
can be regarded as being proved. This rule was first brought into consideration by R. Carnap [1]. Carnap's rule uses an infinite set of premises and is therefore inadmissible within the structure of the formal theories of D. Hilbert. The concept of a derivation in a system with the Carnap rule is undecidable. In mathematical logic one uses, for the study of formal arithmetic, the constructive Carnap rule: If there is an algorithm which for a natural number  provides a derivation of the formula
provides a derivation of the formula 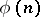 , then the proposition
, then the proposition 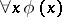 can be regarded as being proved (the restricted
can be regarded as being proved (the restricted 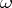 -rule, the rule of constructive infinite induction). Classical arithmetic calculus, which by Gödel's theorem is incomplete, becomes complete on adding the constructive Carnap rule (see [2], [3]).
-rule, the rule of constructive infinite induction). Classical arithmetic calculus, which by Gödel's theorem is incomplete, becomes complete on adding the constructive Carnap rule (see [2], [3]).
References
| [1] | R. Carnap, "The logical syntax of language" , Kegan Paul, Trench & Truber (1937) (Translated from German) |
| [2] | A.V. Kuznetsov, Uspekhi Mat. Nauk , 12 : 4 (1957) pp. 218–219 |
| [3] | J.R. Shoenfield, "On a restricted 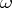 -rule" Bull. Acad. Polon. Sci. Cl. III , 7 (1959) pp. 405–407 -rule" Bull. Acad. Polon. Sci. Cl. III , 7 (1959) pp. 405–407 |
Carnap rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carnap_rule&oldid=12356