Carleson theorem
For a function in 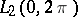 its trigonometric Fourier series converges almost everywhere. This was stated as a conjecture by N.N. Luzin [1] and proved by L. Carleson [2]. The statement of Carleson's theorem is also valid for functions in
its trigonometric Fourier series converges almost everywhere. This was stated as a conjecture by N.N. Luzin [1] and proved by L. Carleson [2]. The statement of Carleson's theorem is also valid for functions in 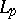 for
for 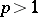 (see [3]). The fact that it does not hold for
(see [3]). The fact that it does not hold for 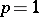 was shown by an example, constructed by A.N. Kolmogorov [4], of a function in
was shown by an example, constructed by A.N. Kolmogorov [4], of a function in 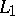 the trigonometric Fourier series of which diverges almost everywhere.
the trigonometric Fourier series of which diverges almost everywhere.
References
| [1] | N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1915) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212) |
| [2] | L. Carleson, "Convergence and growth of partial sums of Fourier series" Acta Math. , 116 (1966) pp. 135–157 |
| [3] | R.A. Hunt, "On the convergence of Fourier series" , Proc. Conf. Orthogonal Expansions and their Continuous Analogues , Southern Illinois Univ. Press (1968) pp. 234–255 |
| [4] | A. [A.N. Kolmogorov] Kolmogoroff, "Une série de Fourier–Lebesgue divergente presque partout" Fund. Math. , 4 (1923) pp. 324–328 |
Comments
Because of [3] the theorem is also referred to as the Carleson–Hunt theorem (cf. [a3], which is a profound exposition of this theorem).
A few years later (than [4]) Kolmogorov anew proved the existence of a function in 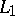 whose trigonometric Fourier series diverges everywhere [a1].
whose trigonometric Fourier series diverges everywhere [a1].
References
| [a1] | A.N. Kolmogorov, "Une série de Fourier–Lebesgue divergent partout" C.R. Acad. Sci. Paris Sér A-B , 183 (1926) pp. 1327–1328 |
| [a2] | C.J. Mozzochi, "On the pointwise convergence of Fourier series" , Lect. notes in math. , 199 , Springer (1970) |
| [a3] | O.G. Jørsboe, L. Mejlbro, "The Carleson–Hunt theorem on Fourier series" , Lect. notes in math. , 911 , Springer (1982) |
Carleson theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carleson_theorem&oldid=11951