Cardinality
cardinal number, of a set 
That property of  which is inherent in any set
which is inherent in any set  equivalent to
equivalent to  . Here two sets are called equivalent (or equipotent or of the same cardinality) if it is possible to construct a one-to-one correspondence between them. Thus, "defining by abstraction" , one may say that cardinality is that which is common to all equivalent sets. Since what is common to all finite sets equivalent to each other is the quantity, or number, of their elements, in its application to infinite sets the idea of cardinality is an analogue of the idea of quantity. The cardinality is a fundamental idea in set theory, due to G. Cantor. A set that is equivalent to the set of all natural numbers is called countable. The corresponding cardinality is denoted by
. Here two sets are called equivalent (or equipotent or of the same cardinality) if it is possible to construct a one-to-one correspondence between them. Thus, "defining by abstraction" , one may say that cardinality is that which is common to all equivalent sets. Since what is common to all finite sets equivalent to each other is the quantity, or number, of their elements, in its application to infinite sets the idea of cardinality is an analogue of the idea of quantity. The cardinality is a fundamental idea in set theory, due to G. Cantor. A set that is equivalent to the set of all natural numbers is called countable. The corresponding cardinality is denoted by  (aleph null). The cardinality of sets equivalent to the set of real numbers is called the cardinality of the continuum and is denoted by
(aleph null). The cardinality of sets equivalent to the set of real numbers is called the cardinality of the continuum and is denoted by  or
or  . For example, the set of all algebraic numbers has countable cardinality, and the set of all closed subsets of
. For example, the set of all algebraic numbers has countable cardinality, and the set of all closed subsets of  -dimensional Euclidean space has the cardinality of the continuum. The Cantor–Bernshtein theorem: If for two sets, each is equivalent to a subset of the other, then the two sets are equivalent. In this case it is said that these sets have the same cardinality. If a set
-dimensional Euclidean space has the cardinality of the continuum. The Cantor–Bernshtein theorem: If for two sets, each is equivalent to a subset of the other, then the two sets are equivalent. In this case it is said that these sets have the same cardinality. If a set  is equivalent to a subset of a set
is equivalent to a subset of a set 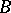 , whereas
, whereas 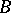 is not equivalent to any subset of
is not equivalent to any subset of 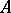 , then it is said that the cardinality of
, then it is said that the cardinality of 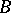 is greater than that of
is greater than that of 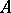 . Cantor's theorem: The cardinality of the set of all subsets of a non-empty set
. Cantor's theorem: The cardinality of the set of all subsets of a non-empty set 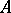 is greater than the cardinality of
is greater than the cardinality of 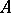 . This theorem allows one to construct a hierarchy of cardinalities (see Cardinal number).
. This theorem allows one to construct a hierarchy of cardinalities (see Cardinal number).
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
Comments
More information and references can be found in the article Cardinal number.
Cardinality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cardinality&oldid=12401