Cap
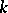 -cap
-cap
A set of 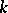 points of a finite projective space
points of a finite projective space 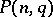 no three of which are collinear. Two caps are considered equivalent if there is a collineation of
no three of which are collinear. Two caps are considered equivalent if there is a collineation of 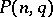 transforming one into the other. The search for the maximal number
transforming one into the other. The search for the maximal number 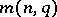 of points of a cap in
of points of a cap in 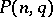 , the construction, and the classification of
, the construction, and the classification of 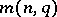 -caps form important problems in the study of caps that are not yet (1984) completely solved. The following results are known (see [2], [3]):
-caps form important problems in the study of caps that are not yet (1984) completely solved. The following results are known (see [2], [3]):
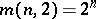 ; the
; the 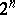 -cap is unique (up to equivalence) and is a set of points not located in a fixed hyperplane in
-cap is unique (up to equivalence) and is a set of points not located in a fixed hyperplane in 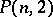 ;
;
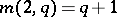 if
if 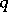 is odd; the
is odd; the 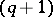 -cap in
-cap in 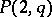 is unique and is a conic;
is unique and is a conic;
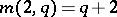 if
if 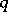 is even; a
is even; a 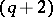 -cap in
-cap in 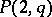 is, generally speaking, not unique;
is, generally speaking, not unique;
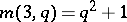 . If
. If 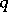 is odd the
is odd the 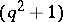 -cap in
-cap in 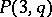 is unique and is an elliptic quadric; if
is unique and is an elliptic quadric; if 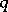 is even it is, generally speaking, not unique;
is even it is, generally speaking, not unique;
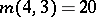 ; a
; a 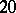 -cap in
-cap in 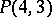 is not unique;
is not unique;
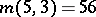 ; the
; the 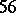 -cap in
-cap in 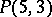 is unique.
is unique.
Caps are used in coding theory (cf., e.g., [2]).
References
| [1] | R.C. Bose, "Mathematical theory of the symmetrical factorial design" Shankhyā , 8 (1947) pp. 107–166 |
| [2] | R. Hill, "Caps and codes" Discrete Math. , 22 : 2 (1978) pp. 111–137 |
| [3] | B. Segre, "Introduction to Galois geometries" Atti Accad. Naz. Lincei Mem. , 8 (1967) pp. 133–236 |
Comments
In the (differential) topology of surfaces a cap of the second kind or cross cap is a  -dimensional manifold with boundary homeomorphic to the Möbius strip used to construct (more complicated) surfaces by removing a disc and replacing it with a cross cap or with a bundle (also called a cap of the first kind). Cf. Theory of surfaces for more details.
-dimensional manifold with boundary homeomorphic to the Möbius strip used to construct (more complicated) surfaces by removing a disc and replacing it with a cross cap or with a bundle (also called a cap of the first kind). Cf. Theory of surfaces for more details.
Cap. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cap&oldid=14827