Cantor manifold
An  -dimensional compact space
-dimensional compact space 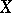 ,
, 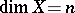 , in which any partition
, in which any partition 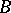 between non-empty sets has dimension
between non-empty sets has dimension 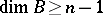 . An equivalent definition is: An
. An equivalent definition is: An  -dimensional Cantor manifold is an
-dimensional Cantor manifold is an  -dimensional compact space
-dimensional compact space 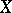 such that for each representation of
such that for each representation of 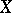 as the union of two non-empty closed proper subsets
as the union of two non-empty closed proper subsets 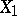 and
and 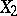 ,
, 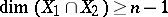 . One-dimensional metrizable Cantor manifolds are one-dimensional continua or Cantor curves (cf. Cantor curve).
. One-dimensional metrizable Cantor manifolds are one-dimensional continua or Cantor curves (cf. Cantor curve).
The concept of a Cantor manifold was introduced by P.S. Urysohn (see [1]). An  -dimensional closed ball, and therefore an
-dimensional closed ball, and therefore an  -dimensional closed manifold, are Cantor manifolds;
-dimensional closed manifold, are Cantor manifolds;  -dimensional Euclidean space cannot be partitioned by a set of dimension
-dimensional Euclidean space cannot be partitioned by a set of dimension 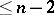 (for
(for 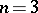 , this is Urysohn's theorem, for
, this is Urysohn's theorem, for 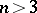 , Aleksandrov's theorem). An
, Aleksandrov's theorem). An 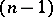 -dimensional Cantor manifold is the common boundary of two regions of
-dimensional Cantor manifold is the common boundary of two regions of  -dimensional Euclidean space, one of which is bounded (Aleksandrov's theorem). The main fact in the theory of Cantor manifolds is that every
-dimensional Euclidean space, one of which is bounded (Aleksandrov's theorem). The main fact in the theory of Cantor manifolds is that every  -dimensional compact space contains an
-dimensional compact space contains an  -dimensional Cantor manifold (Aleksandrov's theorem).
-dimensional Cantor manifold (Aleksandrov's theorem).
A maximal  -dimensional Cantor manifold in an
-dimensional Cantor manifold in an  -dimensional compact space
-dimensional compact space 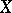 is called a dimensional component of
is called a dimensional component of 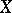 . An
. An  -dimensional Cantor submanifold of a compact Hausdorff space
-dimensional Cantor submanifold of a compact Hausdorff space 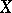 is contained in a unique dimensional component of
is contained in a unique dimensional component of 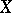 . The intersection of two distinct dimensional components of an
. The intersection of two distinct dimensional components of an  -dimensional compact Hausdorff space
-dimensional compact Hausdorff space 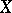 has dimension
has dimension 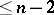 . In particular, dimensional components of a one-dimensional compact Hausdorff space are components of it. The set of dimensional components of a finite-dimensional compact metric space is finite, countable or has the cardinality of the continuum. If
. In particular, dimensional components of a one-dimensional compact Hausdorff space are components of it. The set of dimensional components of a finite-dimensional compact metric space is finite, countable or has the cardinality of the continuum. If 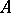 is an arbitrary dimensional component of a perfectly-normal compact space
is an arbitrary dimensional component of a perfectly-normal compact space 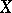 and
and 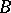 is the union of all remaining dimensional components, then
is the union of all remaining dimensional components, then 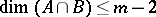 (Aleksandrov's theorem). In a hereditarily-normal first-countable compact Hausdorff space, a dimensional component may be contained in the union of the remaining dimensional components.
(Aleksandrov's theorem). In a hereditarily-normal first-countable compact Hausdorff space, a dimensional component may be contained in the union of the remaining dimensional components.
The union 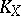 of all dimensional components of an
of all dimensional components of an  -dimensional compact space
-dimensional compact space 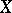 is called the interior dimensional kernel of the space. In view of the monotonicity of dimension, it is always true that
is called the interior dimensional kernel of the space. In view of the monotonicity of dimension, it is always true that 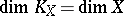 and
and 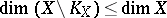 when
when 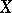 is a perfectly-normal compact space. The set
is a perfectly-normal compact space. The set 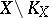 contains no
contains no  -dimensional compact set. But even for Hausdorff compacta it is not known (1978) whether
-dimensional compact set. But even for Hausdorff compacta it is not known (1978) whether 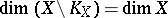 . With regard to hereditarily-normal compact spaces, the interior dimensional kernel and its complement can have all permissible dimensions; that is to say, assuming the validity of the continuum hypothesis, for any triple of integers
. With regard to hereditarily-normal compact spaces, the interior dimensional kernel and its complement can have all permissible dimensions; that is to say, assuming the validity of the continuum hypothesis, for any triple of integers  ,
, 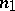 and
and 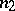 with
with 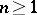 ,
, 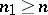 and
and 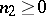 , there exists a hereditarily-normal compact space
, there exists a hereditarily-normal compact space 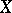 of dimension
of dimension  such that
such that 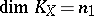 and
and 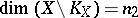 .
.
If 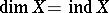 , then
, then 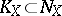 (as defined by Urysohn) is the inductive dimensional kernel, that is, the set of all
(as defined by Urysohn) is the inductive dimensional kernel, that is, the set of all 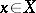 for which
for which 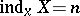 . The inductive dimensional kernel
. The inductive dimensional kernel 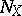 of a compact metric set
of a compact metric set 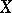 is always an
is always an 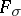 set. It is not known whether the same holds for the interior dimensional kernel. For compact Hausdorff spaces however, neither the inductive dimensional kernel nor the interior dimensional kernel need be an
set. It is not known whether the same holds for the interior dimensional kernel. For compact Hausdorff spaces however, neither the inductive dimensional kernel nor the interior dimensional kernel need be an 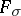 set. At each point
set. At each point 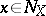 ,
,
 |
if 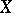 is compact metric (Menger's theorem). Therefore for an arbitrary compact metric space
is compact metric (Menger's theorem). Therefore for an arbitrary compact metric space 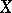 ,
, 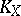 is everywhere dense in
is everywhere dense in 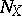 . This does not carry over to arbitrary compact Hausdorff spaces. It remains an open question (1978) whether a point is contained in the inductive dimensional kernel along with some non-degenerate continuum.
. This does not carry over to arbitrary compact Hausdorff spaces. It remains an open question (1978) whether a point is contained in the inductive dimensional kernel along with some non-degenerate continuum.
A finite-dimensional continuum 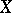 whose interior dimensional kernel
whose interior dimensional kernel 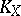 is everywhere dense in
is everywhere dense in 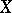 is called a generalized Cantor manifold. The common boundary of two open subsets of
is called a generalized Cantor manifold. The common boundary of two open subsets of  -dimensional Euclidean space is an
-dimensional Euclidean space is an 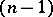 -dimensional generalized Cantor manifold. In a metrizable
-dimensional generalized Cantor manifold. In a metrizable  -dimensional generalized Cantor manifold
-dimensional generalized Cantor manifold 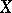 there may be an everywhere-dense set of points
there may be an everywhere-dense set of points  for which
for which 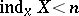 . Neither products nor continuous mappings preserve the property of being a generalized Cantor manifold. The same is true concerning the property of being a Cantor manifold.
. Neither products nor continuous mappings preserve the property of being a generalized Cantor manifold. The same is true concerning the property of being a Cantor manifold.
A compact space 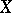 is called an infinite-dimensional Cantor manifold if there is no method of partitioning it by a weakly infinite-dimensional closed subset.
is called an infinite-dimensional Cantor manifold if there is no method of partitioning it by a weakly infinite-dimensional closed subset.
References
| [1] | P.S. Urysohn, "Works on topology and other areas of mathematics" , 1 , Moscow-Leningrad (1951) (In Russian) |
| [2] | P [P.S. Aleksandrov] Alexandroff, "Untersuchungen über Gestalt und lage abqeschlossener Menge beliebiqer Dimension" Ann. of Math. , 30 (1929) pp. 101–187 |
| [3] | P.S. Aleksandrov, "On the dimension of normal spaces" Proc. Royal. Soc. London Ser. A , 189 (1947) pp. 11–39 |
| [4] | P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian) |
| [5] | V.V. Fedorchuk, "On dimensional components of compact spaces" Soviet Math. Dokl. , 15 : 2 (1974) pp. 505–509 Dokl. Akad. Nauk SSSR , 215 : 2 (1974) pp. 289–292 |
| [6] | K. Menger, "Dimensiontheorie" , Teubner (1928) |
| [7] | E.G. Sklyarenko, "Dimensionality properties of infinite-dimensional spaces" Izv. Akad. Nauk SSSR Ser. Mat. , 23 : 2 (1959) pp. 197–212 (In Russian) |
Comments
The theorems attributed to Aleksandrov are not only due to him: The theorem on partitions of  -dimensional Euclidean space is attributed to K. Menger [a5] and Urysohn [a1] and [a2].
-dimensional Euclidean space is attributed to K. Menger [a5] and Urysohn [a1] and [a2].
The Cantor manifold theorem for compact metric spaces is due to W. Hurewicz and Menger [a3] and L.A. Tumarkin [a6]. Aleksandrov generalized it to arbitrary compact Hausdorff spaces in [3]. Finally, the theorem on intersections of dimensional components was proved by S. Mazurkiewicz in [a4] for compact metric spaces, Aleksandrov generalized it to perfectly-normal compact spaces.
It is not true that every infinite-dimensional compact space contains an infinite-dimensional Cantor manifold, as there are many compact metric weakly infinite-dimensional spaces, e.g. the one-point compactification of the topological sum  of cubes of increasing dimension.
of cubes of increasing dimension.
References
| [a1] | P.S. Urysohn, "Mémoire sur les multiplicités cantoriennes" Fund. Math. , 7 (1925) pp. 30–137 |
| [a2] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50 |
| [a3] | W. Hurewicz, K. Menger, "Dimension and Zusammenhangsstuffe" Math. Ann. , 100 (1928) pp. 618–633 |
| [a4] | S. Mazurkiewicz, "Ein Satz über dimensionelle Komponenten" Fund. Math. , 20 (1933) pp. 98–99 |
| [a5] | K. Menger, "Über die dimension von Punktmengen II" Monatsh. für Math. and Phys. , 34 (1926) pp. 137–161 |
| [a6] | L.A. Tumarkin, "Sur la structure dimensionelle des ensembles fermés" C.R. Acad. Paris , 186 (1928) pp. 420–422 |
Cantor manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cantor_manifold&oldid=14407