Canonical product
Weierstrass canonical product
An entire function with a given sequence of complex numbers  as its zeros. Suppose that the zeros
as its zeros. Suppose that the zeros  are arranged in monotone increasing order of their moduli,
are arranged in monotone increasing order of their moduli,  , and have no limit point in the finite plane (a necessary condition), i.e.
, and have no limit point in the finite plane (a necessary condition), i.e.  . Then the canonical product has the form
. Then the canonical product has the form
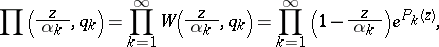 |
where
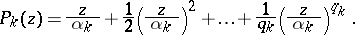 |
The  are called the elementary factors of Weierstrass. The exponents
are called the elementary factors of Weierstrass. The exponents  are chosen so that the canonical product is absolutely and uniformly convergent on any compact set; for example, it suffices to take
are chosen so that the canonical product is absolutely and uniformly convergent on any compact set; for example, it suffices to take  . If the sequence
. If the sequence 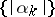 has a finite exponent of convergence
has a finite exponent of convergence
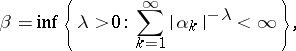 |
then all the 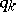 can be chosen to be the same, starting, e.g. from the minimal requirement that
can be chosen to be the same, starting, e.g. from the minimal requirement that  ; this
; this 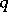 is called the genus of the canonical product. If
is called the genus of the canonical product. If 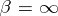 , i.e. if
, i.e. if 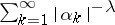 diverges for any
diverges for any 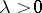 , then one has a canonical product of infinite genus. The order of a canonical product
, then one has a canonical product of infinite genus. The order of a canonical product  (for the definition of the type of a canonical product, see [1]).
(for the definition of the type of a canonical product, see [1]).
References
| [1] | B.Ya. Levin, "The distribution of zeros of entire functions" , Amer. Math. Soc. (1980) (Translated from Russian) |
Comments
See also Blaschke product; Entire function; Hadamard theorem.
Canonical product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Canonical_product&oldid=19024