Campbell-Hausdorff formula
A formula for computing
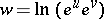 |
in the algebra of formal power series in 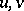 , where the latter are assumed to be associative but non-commutative. More precisely, let
, where the latter are assumed to be associative but non-commutative. More precisely, let 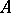 be a free associative algebra with unit over the field
be a free associative algebra with unit over the field 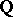 , with free generators
, with free generators  and
and  ; let
; let 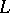 be the Lie subalgebra of
be the Lie subalgebra of 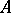 generated by these elements relative to the commutation operation
generated by these elements relative to the commutation operation 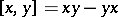 ; and let
; and let 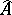 and
and 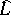 be the natural power series completions of
be the natural power series completions of 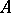 and
and 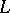 , i.e.
, i.e. 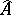 is the ring of power series in the associative but non-commutative variables
is the ring of power series in the associative but non-commutative variables 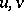 and
and 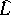 is the closure of
is the closure of 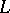 in
in 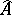 . Then the mapping
. Then the mapping
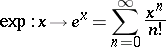 |
is a continuous bijection of 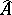 onto the multiplicative group
onto the multiplicative group 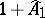 , where
, where 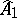 is the set of series without constant term. The inverse of this mapping is
is the set of series without constant term. The inverse of this mapping is
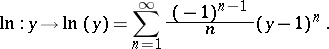 |
The restriction of 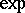 to
to 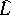 is a bijection of
is a bijection of 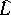 onto the group
onto the group 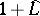 . One can thus introduce a group operation
. One can thus introduce a group operation 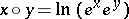 in the set of elements of the Lie algebra
in the set of elements of the Lie algebra 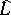 , and it can be shown that the subgroup of this group generated by
, and it can be shown that the subgroup of this group generated by  and
and  is free. The Campbell–Hausdorff formula provides an expression for
is free. The Campbell–Hausdorff formula provides an expression for 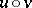 as a power series in
as a power series in  and
and  :
:
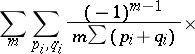 | (*) |
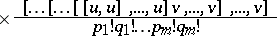 |
(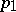 times
times  , then
, then 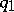 times
times 
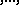
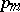 times
times  , then
, then 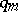 times
times  , in the general term of this series) or (in terms of the adjoint representation
, in the general term of this series) or (in terms of the adjoint representation 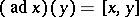 ):
):
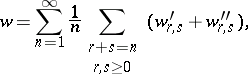 |
where
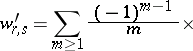 |
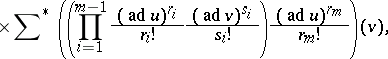 |
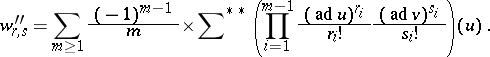 |
Here 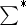 denotes summation over
denotes summation over 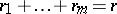 ,
, 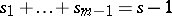 ,
, 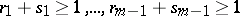 ; and
; and 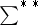 denotes summation over
denotes summation over 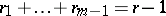 ,
, 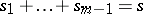 ,
, 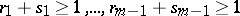 .
.
The first investigation of the expression 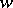 is due to J.E. Campbell . F. Hausdorff [2] proved that
is due to J.E. Campbell . F. Hausdorff [2] proved that 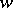 can be expressed in terms of the commutators of
can be expressed in terms of the commutators of  and
and  , i.e. it is an element of the Lie algebra
, i.e. it is an element of the Lie algebra 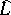 .
.
If 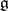 is a normed Lie algebra over a complete non-discretely normed field
is a normed Lie algebra over a complete non-discretely normed field 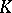 , the series (*), with
, the series (*), with 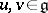 , is convergent in a neighbourhood of zero. Near the zero of
, is convergent in a neighbourhood of zero. Near the zero of 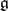 one can thus define the structure of a local Banach Lie group over
one can thus define the structure of a local Banach Lie group over 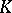 (in the ultrametric case — the structure of a Banach Lie group), with Lie algebra
(in the ultrametric case — the structure of a Banach Lie group), with Lie algebra 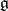 . This yields one of the existence proofs for a local Lie group with a given Lie algebra (Lie's third theorem). Conversely, in any local Lie group multiplication can be expressed in canonical coordinates by the Campbell–Hausdorff formula.
. This yields one of the existence proofs for a local Lie group with a given Lie algebra (Lie's third theorem). Conversely, in any local Lie group multiplication can be expressed in canonical coordinates by the Campbell–Hausdorff formula.
References
| [1a] | J.E. Campbell, Proc. London Math. Soc. , 28 (1897) pp. 381–390 |
| [1b] | J.E. Campbell, Proc. London Math. Soc. , 29 (1898) pp. 14–32 |
| [2] | F. Hausdorff, "Die symbolische Exponential Formel in der Gruppentheorie" Leipziger Ber. , 58 (1906) pp. 19–48 |
| [3] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [4] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) |
| [5] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Ecole Norm. Sup. (1955) |
| [6] | W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations in terms of generators and relations" , Wiley (Interscience) (1966) |
Comments
Let 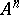 be the component of
be the component of 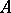 consisting of non-commutative polynomials of degree
consisting of non-commutative polynomials of degree  . Then
. Then 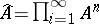 . Similarly
. Similarly  .
.
The formula for 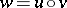 is also known as the Baker–Campbell–Hausdorff formula or Campbell–Baker–Hausdorff formula. The first few terms are:
is also known as the Baker–Campbell–Hausdorff formula or Campbell–Baker–Hausdorff formula. The first few terms are:
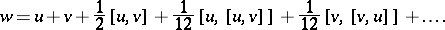 |
The formula in terms of the 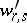 and
and 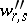 is known as the explicit Campbell–Hausdorff formula (in Dynkin's form).
is known as the explicit Campbell–Hausdorff formula (in Dynkin's form).
References
| [a1] | H.F. Baker, "Alternants and continuous groups" Proc. London Math. Soc. (2) , 3 (1905) pp. 24–47 |
| [a2] | V.S. Varadarajan, "Lie groups, Lie algebras, and their representations" , Springer (1984) pp. Section 2.15 |
Campbell-Hausdorff formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Campbell-Hausdorff_formula&oldid=18290