Calogero-Moser-Krichever system
Calogero–Moser–Sutherland–Krichever system
A finite-dimensional Hamiltonian system which is algebraically completely integrable (cf. Completely-integrable differential equation). It admits several generalizations, which will be indicated below. During the enormous activity on mathematical aspects of integrable systems and soliton equations, starting in the late 1960{}s, some prototypes that represent the main features have emerged. For example, the Korteweg–de Vries equation and the non-linear Schrödinger equation for inverse scattering [a8], rank- perturbations for algebraic complete integrability [a19], [a20], the Kadomtsev–Petviashvili equation (cf. Soliton) for Grassmannians and Schur functions [a30], and the modified Korteweg–de Vries equation for representation theory [a6], [a15].
perturbations for algebraic complete integrability [a19], [a20], the Kadomtsev–Petviashvili equation (cf. Soliton) for Grassmannians and Schur functions [a30], and the modified Korteweg–de Vries equation for representation theory [a6], [a15].
As a prototype, the Calogero–Moser–Krichever system possesses all the standard features of algebraic complete integrability: 1) a Lax pair, spectral curve, and Abelian integrals; 2) a connection with soliton equations; 3) an  -matrix; 4) a geodesic-motion interpretation. However, it has also more unique features: 5) a link with elliptic functions; 6) a more sophisticated interpretation of the Lax pair, giving a link with the Hitchin system, which is a more powerful source of algebraic complete integrability over moduli spaces of vector bundles; 7) the bispectral property.
-matrix; 4) a geodesic-motion interpretation. However, it has also more unique features: 5) a link with elliptic functions; 6) a more sophisticated interpretation of the Lax pair, giving a link with the Hitchin system, which is a more powerful source of algebraic complete integrability over moduli spaces of vector bundles; 7) the bispectral property.
A brief illustration of these terms follows.
1) The system has a Hamiltonian function
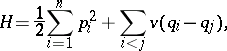 |
where 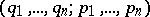 are position/momentum variables (all quantities are complex numbers) and
are position/momentum variables (all quantities are complex numbers) and  is an even function. If
is an even function. If 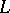 and
and 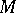 are the
are the 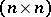 -matrices with entries
-matrices with entries
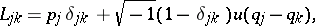 |
 |
where  is odd and
is odd and 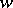 ,
,  are even, then the equation
are even, then the equation 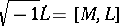 implies
implies 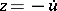 ,
, 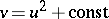 , as well as a functional equation for
, as well as a functional equation for  and
and 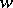 with solutions
with solutions
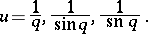 |
These three cases are referred to as rational (Calogero–Moser system), trigonometric (Calogero–Sutherland system) and elliptic (Calogero–Moser–Krichever system), respectively; the first two can be viewed as limits of the third as one or both periods of the Weierstrass function 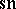 (cf. Weierstrass elliptic functions) tend to infinity. In each case, the invariants
(cf. Weierstrass elliptic functions) tend to infinity. In each case, the invariants 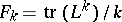 ,
, 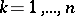 , are (generically) functionally independent and in involution (cf. Integrals in involution), so that the system is completely integrable. This was the first example [a21] of a Lax pair with as parameter a function over a curve of genus
, are (generically) functionally independent and in involution (cf. Integrals in involution), so that the system is completely integrable. This was the first example [a21] of a Lax pair with as parameter a function over a curve of genus 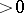 (generalizations are still (1996) quite rare, cf. [a10] for hyperelliptic parameters).
(generalizations are still (1996) quite rare, cf. [a10] for hyperelliptic parameters).
2) By interpolating an eigenvector of  into a Baker–Akhiezer function, it was shown in [a21] that the solutions correspond to elliptic (in
into a Baker–Akhiezer function, it was shown in [a21] that the solutions correspond to elliptic (in  ) solutions of the Kadomtsev–Petviashvili equation
) solutions of the Kadomtsev–Petviashvili equation 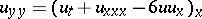 . The first breakthrough in this respect was made in [a1], concerning Korteweg–de Vries solutions and Lamé equations (cf. also Lamé equation); moduli spaces of the corresponding algebro-geometric configurations (tangential covers) were described in [a31] and their density was detected in [a3].
. The first breakthrough in this respect was made in [a1], concerning Korteweg–de Vries solutions and Lamé equations (cf. also Lamé equation); moduli spaces of the corresponding algebro-geometric configurations (tangential covers) were described in [a31] and their density was detected in [a3].
3) Several models of the  -matrix, both dynamic and non-dynamic, recently (1990{}s) became available (for a most complete set of references see [a11]); however a finite-dimensional geodesic motion interpretation 4) has only been achieved for the rational and trigonometric cases [a17].
-matrix, both dynamic and non-dynamic, recently (1990{}s) became available (for a most complete set of references see [a11]); however a finite-dimensional geodesic motion interpretation 4) has only been achieved for the rational and trigonometric cases [a17].
5) S.P. Novikov posed the following question: Which algebro-geometric Kadomtsev–Petviashvili solutions can be expressed in terms of elliptic functions (cf. also Elliptic function)? These non-trivially overlap with elliptic solitons and a state-of-the-art report can be found in [a22].
6) is the deep theory that ensues if the moving data is viewed as a rank- bundle over the elliptic curve, cf. [a4], [a9].
bundle over the elliptic curve, cf. [a4], [a9].
Lastly, 7) is an extra property of the Baker function in the rational case, defined by F.A. Grünbaum [a7] in connection with computerized tomography (roughly stated, the Baker function is both an  - and a
- and a  -eigenfunction for a pair of operators with eigenvalues that are functions of
-eigenfunction for a pair of operators with eigenvalues that are functions of  ,
,  , respectively); its manifestation for the matrix
, respectively); its manifestation for the matrix  above (cf. [a1]) is investigated in [a16].
above (cf. [a1]) is investigated in [a16].
A final word about generalizations: [a27] adapts the geodesic problem 4) to other groups and metrics; [a28] defines a relativistic Calogero–Moser–Krichever system; [a24] and [a25] provide discretized versions of the Calogero–Moser–Krichever and Ruijsenaars system, respectively; an Euler Calogero–Moser–Krichever system is related to a multi-component Kadomtsev–Petviashvili equation in [a23]; and the most recent application of the Calogero–Moser–Krichever system is that conjecturally it provides moduli for solutions to the Seiberg–Witten equations, [a5].
References
| [a1] | H. Airault, H.P. McKean, J. Moser, "Rational and elliptic solutions of the Korteweg–de Vries equation and a related many-body problem" Commun. Pure Appl. Math. , 30 (1977) pp. 95–148 |
| [a2] | E.D. Belokolos, V.Z. Enol'skii, "Algebraically integrable nonlinear equations and Humbert surfaces, plasma theory and nonlinear and turbulent processes in physics" , 1–2 , World Sci. (1988) pp. 20–57 |
| [a3] | E. Colombo, G.P. Pirola, E. Previato, "Density of elliptic solitons" J. Reine Angew. Math. , 451 (1994) pp. 161–169 |
| [a4] | R. Donagi, E. Markman, "Spectral covers, algebraically completely integrable Hamiltonian systems, and moduli of bundles" , Integrable Systems and Quantum Groups , Lecture Notes in Mathematics , 1620 , Springer (1996) |
| [a5] | R. Donagi, E. Witten, "Supersymmetric Yang–Mills systems and integrable systems" hep-th/9510101 (1995) |
| [a6] | V.G. Drinfeld, V.V. Sokolov, "Lie algebras and equations of Korteweg–de Vries type" J. Soviet Math. , 30 (1985) pp. 1975–2005 |
| [a7] | J.J. Duistermaat, F.A. Grünbaum, "Differential equations in the spectral parameter" Comm. Math. Phys. , 103 (1986) pp. 177–240 |
| [a8] | L.D. Faddeev, L.A. Takhtajan, "Hamiltonian methods in the theory of solitons" , Springer (1987) |
| [a9] | G. Faltings, "Stable  -bundles and projective connections" J. Algebraic Geom. , 2 (1993) pp. 507–568 -bundles and projective connections" J. Algebraic Geom. , 2 (1993) pp. 507–568 |
| [a10] | Yu.N. Fedorov, "Integrable systems, Lax representations, and confocal quadrics" Amer. Math. Soc. Transl. Ser. 2 , 168 (1995) pp. 173–199 |
| [a11] | K. Hasegawa, "Ruijsenaars' commuting difference operators as commuting transfer matrices" q-alg/9512029 (1995) |
| [a12] | N. Hitchin, "Stable bundles and integrable systems" Duke Math. J. , 54 (1987) pp. 91–114 |
| [a13] | E.L. Ince, "Further investigations into the periodic Lamé function" Proc. Roy. Soc. Edinburgh , 60 (1940) pp. 83–99 |
| [a14] | A.R. Its, V.Z. Enol'skii, "Dynamics of the Calogero–Moser system and the reduction of hyperelliptic integrals to elliptic integrals" Funct. Anal. Appl. , 20 (1986) pp. 62–64 |
| [a15] | V.G. Kac, J.W. van de Leur, "The  -component KP hierarchy and representation theory" , Important Developments in Soliton Theory , Springer (1993) pp. 302–343 -component KP hierarchy and representation theory" , Important Developments in Soliton Theory , Springer (1993) pp. 302–343 |
| [a16] | A. Kasman, "Bispectral KP solutions and linearization of Calogero–Moser particle systems" Comm. Math. Phys. , 172 (1995) pp. 427–448 |
| [a17] | D. Kazhdan, B. Kostant, S. Sternberg, "Hamiltonian group actions and dynamical systems of Calogero type" Comm. Pure Appl. Math. , 31 (1978) pp. 481–507 |
| [a18] | I.M. Krichever, "Rational solutions of the Kadomtsev–Petviashvili equation and integrable systems of  particles on a line" Funct. Anal. Appl. , 12 (1978) pp. 59–61 particles on a line" Funct. Anal. Appl. , 12 (1978) pp. 59–61 |
| [a19] | M. Adler, P. van Moerbeke, "Completely integrable systems, Euclidean Lie algebras, and curves" Adv. in Math. , 38 (1980) pp. 267–317 |
| [a20] | M. Adler, P. van Moerbeke, "Linearization of Hamiltonian systems, Jacobi varieties and representation theory" Adv. in Math. , 38 (1980) pp. 318–379 |
| [a21] | I.M. Krichever, "Elliptic solutions of the KP equation and integrable systems of particles" Funct. Anal. Appl. , 14 (1980) pp. 282–290 |
| [a22] | I.M. (ed.) Krichever, "Special issue on elliptic solitons, dedicated to the memory of J.-L. Verdier" Acta Applic. Math. , 36 : 1–2 (1994) |
| [a23] | I.M. Krichever, O. Babelon, E. Billey, M. Talon, "Spin generalizations of the Calogero–Moser system and the matrix KP equation" Amer. Math. Soc. Transl. Ser. 2 , 170 (1995) pp. 83–119 |
| [a24] | F.W. Nijhoff, G.-D. Pang, "A time-discretized version of the Calogero–Moser model" Phys. Lett. A , 191 (1994) pp. 101–107 |
| [a25] | F.W. Nijhoff, O. Ragnisco, V.B. Kuznetsov, "Integrable time-discretisation of the Ruijsenaars–Schneider model" Comm. Math. Phys. , 176 (1996) pp. 681–700 |
| [a26] | S.P. Novikov, "A periodic problem for the KdV equation" Funct. Anal. Appl. , 8 (1974) pp. 236–246 |
| [a27] | M.A. Olshanetsky, A.M. Perelomov, "Classical integrable finite-dimensional systems related to Lie algebras" Phys. Rep. , 71 (1981) pp. 313–400 |
| [a28] | S.N.M. Ruijsenaars, "Complete integrability of relativistic Calogero–Moser systems and elliptic function identities" Comm. Math. Phys. , 20 (1987) pp. 191–213 |
| [a29] | G. Segal, G. Wilson, "Loop groups and equations of KdV type" IHES Publ. Math. , 61 (1985) pp. 5–65 |
| [a30] | M. Sato, Y. Sato, "Soliton equations as dynamical systems on infinite-dimensional Grassmann manifold" , Nonlinear Partial Differential Equations in Applied Science , Math. Stud. , 81 , North-Holland (1983) pp. 259–271 |
| [a31] | A. Treibich, J.-L. Verdier, "Solitons elliptiques" , The Grothendieck Festschrift , III , Birkhäuser (1990) pp. 437–480 |
| [a32] | A.P. Veselov, "Rational solutions of the KP equation and hamiltonian systems" Russian Math. Surveys , 35 : 1 (1980) pp. 239–240 |
Calogero-Moser-Krichever system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Calogero-Moser-Krichever_system&oldid=18918