Difference between revisions of "Calderón couples"
Ulf Rehmann (talk | contribs) m (moved Calderon couples to Calderón couples over redirect: accented title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c1100101.png | ||
| + | $#A+1 = 127 n = 11 | ||
| + | $#C+1 = 127 : ~/encyclopedia/old_files/data/C110/C.1100010 Calder\Aeon couples | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Let $ A _ {0} $ | |
| + | and $ A _ {1} $ | ||
| + | be two Banach spaces (cf. [[Banach space|Banach space]]) embedded in a Hausdorff [[Topological vector space|topological vector space]]. Such a pair of spaces is termed a Banach couple or Banach pair. The theory of [[Interpolation of operators|interpolation of operators]] provides a variety of interpolation methods or interpolation functors for generating interpolation spaces with respect to any such couple $ ( A _ {0} ,A _ {1} ) $, | ||
| + | namely normed spaces $ A $( | ||
| + | cf. [[Normed space|Normed space]]) having the property that every [[Linear operator|linear operator]] $ T : {A _ {0} + A _ {1} } \rightarrow {A _ {0} + A _ {1} } $ | ||
| + | such that $ T : {A _ {j} } \rightarrow {A _ {j} } $ | ||
| + | boundedly for $ j = 0,1 $ | ||
| + | also maps $ A $ | ||
| + | to $ A $ | ||
| + | boundedly. | ||
| − | + | A fundamental problem in interpolation theory is the description of all interpolation spaces with respect to a given Banach pair $ ( A _ {0} ,A _ {1} ) $. | |
| + | In the 1960s, A.P. Calderón [[#References|[a4]]] and B.S. Mityagin [[#References|[a10]]] independently gave characterizations of all interpolation spaces $ A $ | ||
| + | with respect to the particular couple $ ( A _ {0} ,A _ {1} ) = ( L _ {1} , L _ \infty ) $. | ||
| + | Calderón showed that $ A $ | ||
| + | is an interpolation space if and only if it has the following monotonicity property: For every element $ a \in A $ | ||
| + | and every element $ b \in A _ {0} + A _ {1} $, | ||
| + | whenever $ K ( t,b ) \leq K ( t,a ) $ | ||
| + | for all $ t > 0 $, | ||
| + | it follows that $ b \in A $ | ||
| + | and $ \| b \| _ {A} \leq C \| a \| _ {A} $ | ||
| + | for some absolute constant $ C $. | ||
| − | + | Here, $ K ( t,f ) = K ( t,f;A _ {0} ,A _ {1} ) $ | |
| + | denotes the Peetre $ K $- | ||
| + | functional of $ f $ | ||
| + | with respect to the couple $ ( A _ {0} ,A _ {1} ) $. | ||
| + | In this particular case, where the couple is $ ( L _ {1} ,L _ \infty ) $, | ||
| + | there is a concrete formula for $ K ( t,x ) $( | ||
| + | cf. [[Interpolation of operators|Interpolation of operators]] for further details). | ||
| − | + | Mityagin's result, though of course ultimately equivalent to Calderón's, is formulated differently, in terms of the effect of measure-preserving transformations and multiplication by unimodular functions on elements of $ A $. | |
| − | + | The work of Calderón and Mityagin triggered a long series of papers by many mathematicians (many of these are listed in [[#References|[a2]]] and in [[#References|[a5]]]) in which it was shown that all the interpolation spaces of many other Banach pairs $ ( A _ {0} ,A _ {1} ) $ | |
| + | can also be characterized via the Peetre $ K $- | ||
| + | functionals for those pairs, by a monotonicity condition exactly analogous to the one in Calderón's result above. The Banach pairs $ ( A _ {0} ,A _ {1} ) $ | ||
| + | for which such a characterization holds are often referred to as Calderón couples or Calderón pairs. (They are also sometimes referred to using other terminology, such as Calderón–Mityagin couples, $ K $- | ||
| + | monotone couples or $ {\mathcal C} $- | ||
| + | pairs.) | ||
| − | + | It is also convenient to use the terminology $ K $- | |
| + | space for any normed space $ A $ | ||
| + | satisfying $ A _ {0} \cap A _ {1} \subset A \subset A _ {0} + A _ {1} $ | ||
| + | as well as the above-mentioned monotonicity property with respect to the $ K $- | ||
| + | functional for $ ( A _ {0} ,A _ {1} ) $. | ||
| + | By the important $ K $- | ||
| + | divisibility theorem of Yu.A Brudnyi and N.Ya. Kruglyak [[#References|[a2]]], it follows that each such $ K $- | ||
| + | space necessarily coincides, to within equivalence of norms, with a space of the special form $ ( A _ {0} ,A _ {1} ) _ {G} ^ {K} $( | ||
| + | as defined in [[Interpolation of operators|Interpolation of operators]]). Thus, for Calderón pairs, all the interpolation spaces are of this relatively simple form. | ||
| − | + | So, one can remark that, roughly speaking, for a Banach pair $ ( A _ {0} ,A _ {1} ) $ | |
| + | to be Calderón, the class of its interpolation spaces has to be relatively small, and correspondingly, the family of linear operators which are bounded on both $ A _ {0} $ | ||
| + | and $ A _ {1} $ | ||
| + | has to be relatively large. | ||
| − | + | Those Banach pairs which are known to be Calderón include pairs $ ( L _ {p _ {0} } ( w _ {0} ) ,L _ {p _ {1} } ( w _ {1} ) ) $ | |
| + | of weighted $ L _ {p} $ | ||
| + | spaces for all choices of weight functions and for all exponents $ p _ {0} , p _ {1} \in [ 1, \infty ] $( | ||
| + | the Sparr theorem, [[#References|[a12]]]). Other examples include all Banach pairs of Hilbert spaces, various pairs of Hardy spaces, or of Lorentz or Marcinkiewicz spaces and all "iterated" pairs of the form | ||
| − | + | $$ \tag{a1 } | |
| + | ( A _ {0} ,A _ {1} ) = \left ( ( B _ {0} ,B _ {1} ) _ {\theta _ {0} ,q _ {0} } ^ {K} , ( B _ {0} ,B _ {1} ) _ {\theta _ {1} , q _ {1} } ^ {K} \right ) . | ||
| + | $$ | ||
| + | |||
| + | In this last example $ ( B _ {0} ,B _ {1} ) $ | ||
| + | can be taken to be an arbitrary Banach pair and $ \theta _ {j} \in ( 0,1 ) $ | ||
| + | and $ q _ {j} \in [ 1, \infty ] $ | ||
| + | can be arbitrary numbers. Here, $ ( B _ {0} ,B _ {1} ) _ {\theta,q } ^ {K} $ | ||
| + | denotes the Lions–Peetre real-method interpolation space, consisting of all elements $ b \in B _ {0} + B _ {1} $ | ||
| + | for which the norm | ||
| + | |||
| + | $$ | ||
| + | \left \| b \right \| = \left \{ \int\limits _ { 0 } ^ \infty {( t ^ {- \theta } K ( t,b;B _ {0} ,B _ {1} ) ) ^ {q} } { { | ||
| + | \frac{dt }{t} | ||
| + | } } \right \} ^ { {1 / q } } | ||
| + | $$ | ||
is finite. | is finite. | ||
| − | By choosing particular pairs | + | By choosing particular pairs $ ( B _ {0} ,B _ {1} ) $ |
| + | one obtains, as special cases of this last result, that various pairs of Besov spaces (cf. [[Imbedding theorems|Imbedding theorems]]) or Lorentz $ L _ {p,q } $ | ||
| + | spaces or Schatten operator ideals are all Calderón. | ||
| − | In parallel with all these positive results it has also been shown that many Banach pairs fail to be Calderón. These include | + | In parallel with all these positive results it has also been shown that many Banach pairs fail to be Calderón. These include $ ( L _ {p} ( \mathbf R ^ {n} ) , W _ {p} ^ {1} ( \mathbf R ^ {n} ) ) $ |
| + | where $ p \neq 2 $( | ||
| + | here $ W _ {p} ^ {1} $ | ||
| + | is a [[Sobolev space|Sobolev space]]) and $ ( C ( [ 0,1 ] ) , { \mathop{\rm Lip} } ( [ 0,1 ] ) ) $ | ||
| + | and also such simple pairs as $ ( {\mathcal l} _ {1} \oplus {\mathcal l} _ {2} , {\mathcal l} _ \infty \oplus {\mathcal l} _ \infty ) $ | ||
| + | and $ ( L _ {1} + L _ \infty ,L _ {1} \cap L _ \infty ) $. | ||
| − | In [[#References|[a3]]], Brudnyi and A. Shteinberg consider whether pairs of the form | + | In [[#References|[a3]]], Brudnyi and A. Shteinberg consider whether pairs of the form $ ( F _ {0} ( B _ {0} ,B _ {1} ) ,F _ {1} ( B _ {0} ,B _ {1} ) ) $ |
| + | are Calderón, where $ F _ {0} $ | ||
| + | and $ F _ {1} $ | ||
| + | are interpolation functors (cf. [[Interpolation of operators|Interpolation of operators]]). Their results for the pair $ ( B _ {0} ,B _ {1} ) = ( C ( [ 0,1 ] ) , { \mathop{\rm Lip} } ( [ 0,1 ] ) ) $ | ||
| + | lead them to conjecture that the above-mentioned result about iterated pairs of the form (a1) cannot be extended, i.e., that $ ( F _ {0} ( B _ {0} ,B _ {1} ) ,F _ {1} ( B _ {0} ,B _ {1} ) ) $ | ||
| + | is Calderón for every Banach pair $ ( B _ {0} ,B _ {1} ) $ | ||
| + | if and only if both functors $ F _ {j} $ | ||
| + | are of the form $ F _ {j} ( B _ {0} ,B _ {1} ) = ( B _ {0} ,B _ {1} ) _ {\theta _ {j} ,q _ {j} } ^ {K} $. | ||
| + | As they also remark, all Calderón pairs which have so far (1996) been identified are either couples of Banach lattices of measurable functions on a given measure space, or are obtained from such lattice couples as partial retracts or $ K $- | ||
| + | subcouples. One can ask whether this might in fact be true for all Calderón pairs. | ||
| − | N.J. Kalton [[#References|[a7]]] has given very extensive results about pairs of rearrangement-invariant spaces which are or are not Calderón, including a characterization of all rearrangement-invariant spaces | + | N.J. Kalton [[#References|[a7]]] has given very extensive results about pairs of rearrangement-invariant spaces which are or are not Calderón, including a characterization of all rearrangement-invariant spaces $ X $ |
| + | for which $ ( X,L _ \infty ) $ | ||
| + | is Calderón. Kalton's results, and also the following general negative result from [[#References|[a5]]], suggest that in some sense the Calderón property is very much linked to the spaces of the pair having some sort of $ L _ {p} $ | ||
| + | structure or "near-Lp" structure. This result also shows that Sparr's theorem for weighted $ L _ {p} $ | ||
| + | spaces cannot be sharpened: Let $ {( X _ {0} ,X _ {1} ) } $ | ||
| + | be a pair of saturated $ \sigma $- | ||
| + | order continuous Banach lattices with the Fatou property on the non-atomic measure space $ ( \Omega, \Sigma, \mu ) $. | ||
| + | Suppose that at least one of the spaces $ X _ {0} $ | ||
| + | and $ X _ {1} $ | ||
| + | does not coincide, to within equivalence of norms, with a weighted $ L ^ {p} $ | ||
| + | space on $ \Omega $. | ||
| + | Then there exist weight functions $ {w _ {j} } : \Omega \rightarrow {( 0, \infty ) } $ | ||
| + | for $ j = 0,1 $ | ||
| + | such that the weighted Banach pair $ ( X _ {0} ( w _ {0} ) ,X _ {1} ( w _ {1} ) ) $ | ||
| + | is not Calderón. | ||
| − | In most known examples of Banach pairs | + | In most known examples of Banach pairs $ ( A _ {0} ,A _ {1} ) $ |
| + | which are not Calderón, this happens because the complex interpolation spaces $ [ A _ {0} ,A _ {1} ] _ \alpha $( | ||
| + | see [[Interpolation of operators|Interpolation of operators]]) are not $ K $- | ||
| + | spaces. But M. Mastyło and V.I. Ovchinnikov have found examples (see [[#References|[a9]]]) of non-Calderón couples for which all the spaces $ [ A _ {0} ,A _ {1} ] _ \alpha $ | ||
| + | are $ K $- | ||
| + | spaces. | ||
| − | The notion of Calderón couples can also be considered in the wider context of operators | + | The notion of Calderón couples can also be considered in the wider context of operators $ T $ |
| + | mapping from the spaces of one Banach pair $ ( A _ {0} ,A _ {1} ) $ | ||
| + | to a possibly different Banach pair $ ( B _ {0} ,B _ {1} ) $. | ||
| + | In such a context one says that $ A $ | ||
| + | and $ B $ | ||
| + | are relative interpolation spaces if every linear mapping $ T : {A _ {0} + A _ {1} } \rightarrow {B _ {0} + B _ {1} } $ | ||
| + | which maps $ A _ {j} $ | ||
| + | boundedly into $ B _ {j} $ | ||
| + | for $ j = 0,1 $ | ||
| + | also maps $ A $ | ||
| + | boundedly into $ B $. | ||
| + | (In the notation of [[Interpolation of operators|Interpolation of operators]], $ \{ A _ {0} ,A _ {1} ,A \} $ | ||
| + | is an interpolation triple relative to $ \{ B _ {0} ,B _ {1} ,B \} $.) | ||
| + | One says that $ A $ | ||
| + | and $ B $ | ||
| + | are relative $ K $- | ||
| + | spaces if, for all $ a \in A $ | ||
| + | and $ b \in B _ {0} + B _ {1} $, | ||
| + | the $ K $- | ||
| + | functional inequality | ||
| − | + | $$ | |
| + | K ( t,b;B _ {0} ,B _ {1} ) \leq K ( t,a;A _ {0} ,A _ {1} ) \textrm{ for all } t > 0 | ||
| + | $$ | ||
| − | implies that | + | implies that $ b \in B $ |
| + | with $ \| b \| _ {B} \leq C \| a \| _ {A} $. | ||
| − | + | $ ( A _ {0} ,A _ {1} ) $ | |
| + | and $ ( B _ {0} ,B _ {1} ) $ | ||
| + | are said to be relative Calderón couples if $ A $ | ||
| + | and $ B $ | ||
| + | are relative interpolation spaces if and only if they are relative $ K $- | ||
| + | spaces. J. Peetre has shown (see [[#References|[a6]]]) that if $ ( B _ {0} ,B _ {1} ) $ | ||
| + | is any pair of weighted $ L _ \infty $ | ||
| + | spaces, then $ ( A _ {0} ,A _ {1} ) $ | ||
| + | and $ ( B _ {0} ,B _ {1} ) $ | ||
| + | are relative Calderón couples for all Banach pairs $ ( A _ {0} ,A _ {1} ) $. | ||
| + | Dually, if $ ( A _ {0} ,A _ {1} ) $ | ||
| + | is an arbitrary pair of weighted $ L _ {1} $ | ||
| + | spaces, then $ ( A _ {0} ,A _ {1} ) $ | ||
| + | and $ ( B _ {0} ,B _ {1} ) $ | ||
| + | are relative Calderón couples for all Banach pairs $ ( B _ {0} ,B _ {1} ) $ | ||
| + | satisfying a mild "closure" condition. This latter result is another consequence of the Brudnyi–Kruglyak $ K $- | ||
| + | divisibility theorem. | ||
Finally, given that there are so many cases of couples whose interpolation spaces cannot be all characterized by a Calderón-style condition, one must also seek alternative ways to characterize interpolation spaces. See [[#References|[a11]]] and [[#References|[a8]]] for some special cases. (Cf. also [[#References|[a1]]].) | Finally, given that there are so many cases of couples whose interpolation spaces cannot be all characterized by a Calderón-style condition, one must also seek alternative ways to characterize interpolation spaces. See [[#References|[a11]]] and [[#References|[a8]]] for some special cases. (Cf. also [[#References|[a1]]].) | ||
Revision as of 06:29, 30 May 2020
Let $ A _ {0} $
and $ A _ {1} $
be two Banach spaces (cf. Banach space) embedded in a Hausdorff topological vector space. Such a pair of spaces is termed a Banach couple or Banach pair. The theory of interpolation of operators provides a variety of interpolation methods or interpolation functors for generating interpolation spaces with respect to any such couple $ ( A _ {0} ,A _ {1} ) $,
namely normed spaces $ A $(
cf. Normed space) having the property that every linear operator $ T : {A _ {0} + A _ {1} } \rightarrow {A _ {0} + A _ {1} } $
such that $ T : {A _ {j} } \rightarrow {A _ {j} } $
boundedly for $ j = 0,1 $
also maps $ A $
to $ A $
boundedly.
A fundamental problem in interpolation theory is the description of all interpolation spaces with respect to a given Banach pair $ ( A _ {0} ,A _ {1} ) $. In the 1960s, A.P. Calderón [a4] and B.S. Mityagin [a10] independently gave characterizations of all interpolation spaces $ A $ with respect to the particular couple $ ( A _ {0} ,A _ {1} ) = ( L _ {1} , L _ \infty ) $. Calderón showed that $ A $ is an interpolation space if and only if it has the following monotonicity property: For every element $ a \in A $ and every element $ b \in A _ {0} + A _ {1} $, whenever $ K ( t,b ) \leq K ( t,a ) $ for all $ t > 0 $, it follows that $ b \in A $ and $ \| b \| _ {A} \leq C \| a \| _ {A} $ for some absolute constant $ C $.
Here, $ K ( t,f ) = K ( t,f;A _ {0} ,A _ {1} ) $ denotes the Peetre $ K $- functional of $ f $ with respect to the couple $ ( A _ {0} ,A _ {1} ) $. In this particular case, where the couple is $ ( L _ {1} ,L _ \infty ) $, there is a concrete formula for $ K ( t,x ) $( cf. Interpolation of operators for further details).
Mityagin's result, though of course ultimately equivalent to Calderón's, is formulated differently, in terms of the effect of measure-preserving transformations and multiplication by unimodular functions on elements of $ A $.
The work of Calderón and Mityagin triggered a long series of papers by many mathematicians (many of these are listed in [a2] and in [a5]) in which it was shown that all the interpolation spaces of many other Banach pairs $ ( A _ {0} ,A _ {1} ) $ can also be characterized via the Peetre $ K $- functionals for those pairs, by a monotonicity condition exactly analogous to the one in Calderón's result above. The Banach pairs $ ( A _ {0} ,A _ {1} ) $ for which such a characterization holds are often referred to as Calderón couples or Calderón pairs. (They are also sometimes referred to using other terminology, such as Calderón–Mityagin couples, $ K $- monotone couples or $ {\mathcal C} $- pairs.)
It is also convenient to use the terminology $ K $- space for any normed space $ A $ satisfying $ A _ {0} \cap A _ {1} \subset A \subset A _ {0} + A _ {1} $ as well as the above-mentioned monotonicity property with respect to the $ K $- functional for $ ( A _ {0} ,A _ {1} ) $. By the important $ K $- divisibility theorem of Yu.A Brudnyi and N.Ya. Kruglyak [a2], it follows that each such $ K $- space necessarily coincides, to within equivalence of norms, with a space of the special form $ ( A _ {0} ,A _ {1} ) _ {G} ^ {K} $( as defined in Interpolation of operators). Thus, for Calderón pairs, all the interpolation spaces are of this relatively simple form.
So, one can remark that, roughly speaking, for a Banach pair $ ( A _ {0} ,A _ {1} ) $ to be Calderón, the class of its interpolation spaces has to be relatively small, and correspondingly, the family of linear operators which are bounded on both $ A _ {0} $ and $ A _ {1} $ has to be relatively large.
Those Banach pairs which are known to be Calderón include pairs $ ( L _ {p _ {0} } ( w _ {0} ) ,L _ {p _ {1} } ( w _ {1} ) ) $ of weighted $ L _ {p} $ spaces for all choices of weight functions and for all exponents $ p _ {0} , p _ {1} \in [ 1, \infty ] $( the Sparr theorem, [a12]). Other examples include all Banach pairs of Hilbert spaces, various pairs of Hardy spaces, or of Lorentz or Marcinkiewicz spaces and all "iterated" pairs of the form
$$ \tag{a1 } ( A _ {0} ,A _ {1} ) = \left ( ( B _ {0} ,B _ {1} ) _ {\theta _ {0} ,q _ {0} } ^ {K} , ( B _ {0} ,B _ {1} ) _ {\theta _ {1} , q _ {1} } ^ {K} \right ) . $$
In this last example $ ( B _ {0} ,B _ {1} ) $ can be taken to be an arbitrary Banach pair and $ \theta _ {j} \in ( 0,1 ) $ and $ q _ {j} \in [ 1, \infty ] $ can be arbitrary numbers. Here, $ ( B _ {0} ,B _ {1} ) _ {\theta,q } ^ {K} $ denotes the Lions–Peetre real-method interpolation space, consisting of all elements $ b \in B _ {0} + B _ {1} $ for which the norm
$$ \left \| b \right \| = \left \{ \int\limits _ { 0 } ^ \infty {( t ^ {- \theta } K ( t,b;B _ {0} ,B _ {1} ) ) ^ {q} } { { \frac{dt }{t} } } \right \} ^ { {1 / q } } $$
is finite.
By choosing particular pairs $ ( B _ {0} ,B _ {1} ) $ one obtains, as special cases of this last result, that various pairs of Besov spaces (cf. Imbedding theorems) or Lorentz $ L _ {p,q } $ spaces or Schatten operator ideals are all Calderón.
In parallel with all these positive results it has also been shown that many Banach pairs fail to be Calderón. These include $ ( L _ {p} ( \mathbf R ^ {n} ) , W _ {p} ^ {1} ( \mathbf R ^ {n} ) ) $ where $ p \neq 2 $( here $ W _ {p} ^ {1} $ is a Sobolev space) and $ ( C ( [ 0,1 ] ) , { \mathop{\rm Lip} } ( [ 0,1 ] ) ) $ and also such simple pairs as $ ( {\mathcal l} _ {1} \oplus {\mathcal l} _ {2} , {\mathcal l} _ \infty \oplus {\mathcal l} _ \infty ) $ and $ ( L _ {1} + L _ \infty ,L _ {1} \cap L _ \infty ) $.
In [a3], Brudnyi and A. Shteinberg consider whether pairs of the form $ ( F _ {0} ( B _ {0} ,B _ {1} ) ,F _ {1} ( B _ {0} ,B _ {1} ) ) $ are Calderón, where $ F _ {0} $ and $ F _ {1} $ are interpolation functors (cf. Interpolation of operators). Their results for the pair $ ( B _ {0} ,B _ {1} ) = ( C ( [ 0,1 ] ) , { \mathop{\rm Lip} } ( [ 0,1 ] ) ) $ lead them to conjecture that the above-mentioned result about iterated pairs of the form (a1) cannot be extended, i.e., that $ ( F _ {0} ( B _ {0} ,B _ {1} ) ,F _ {1} ( B _ {0} ,B _ {1} ) ) $ is Calderón for every Banach pair $ ( B _ {0} ,B _ {1} ) $ if and only if both functors $ F _ {j} $ are of the form $ F _ {j} ( B _ {0} ,B _ {1} ) = ( B _ {0} ,B _ {1} ) _ {\theta _ {j} ,q _ {j} } ^ {K} $. As they also remark, all Calderón pairs which have so far (1996) been identified are either couples of Banach lattices of measurable functions on a given measure space, or are obtained from such lattice couples as partial retracts or $ K $- subcouples. One can ask whether this might in fact be true for all Calderón pairs.
N.J. Kalton [a7] has given very extensive results about pairs of rearrangement-invariant spaces which are or are not Calderón, including a characterization of all rearrangement-invariant spaces $ X $ for which $ ( X,L _ \infty ) $ is Calderón. Kalton's results, and also the following general negative result from [a5], suggest that in some sense the Calderón property is very much linked to the spaces of the pair having some sort of $ L _ {p} $ structure or "near-Lp" structure. This result also shows that Sparr's theorem for weighted $ L _ {p} $ spaces cannot be sharpened: Let $ {( X _ {0} ,X _ {1} ) } $ be a pair of saturated $ \sigma $- order continuous Banach lattices with the Fatou property on the non-atomic measure space $ ( \Omega, \Sigma, \mu ) $. Suppose that at least one of the spaces $ X _ {0} $ and $ X _ {1} $ does not coincide, to within equivalence of norms, with a weighted $ L ^ {p} $ space on $ \Omega $. Then there exist weight functions $ {w _ {j} } : \Omega \rightarrow {( 0, \infty ) } $ for $ j = 0,1 $ such that the weighted Banach pair $ ( X _ {0} ( w _ {0} ) ,X _ {1} ( w _ {1} ) ) $ is not Calderón.
In most known examples of Banach pairs $ ( A _ {0} ,A _ {1} ) $ which are not Calderón, this happens because the complex interpolation spaces $ [ A _ {0} ,A _ {1} ] _ \alpha $( see Interpolation of operators) are not $ K $- spaces. But M. Mastyło and V.I. Ovchinnikov have found examples (see [a9]) of non-Calderón couples for which all the spaces $ [ A _ {0} ,A _ {1} ] _ \alpha $ are $ K $- spaces.
The notion of Calderón couples can also be considered in the wider context of operators $ T $ mapping from the spaces of one Banach pair $ ( A _ {0} ,A _ {1} ) $ to a possibly different Banach pair $ ( B _ {0} ,B _ {1} ) $. In such a context one says that $ A $ and $ B $ are relative interpolation spaces if every linear mapping $ T : {A _ {0} + A _ {1} } \rightarrow {B _ {0} + B _ {1} } $ which maps $ A _ {j} $ boundedly into $ B _ {j} $ for $ j = 0,1 $ also maps $ A $ boundedly into $ B $. (In the notation of Interpolation of operators, $ \{ A _ {0} ,A _ {1} ,A \} $ is an interpolation triple relative to $ \{ B _ {0} ,B _ {1} ,B \} $.) One says that $ A $ and $ B $ are relative $ K $- spaces if, for all $ a \in A $ and $ b \in B _ {0} + B _ {1} $, the $ K $- functional inequality
$$ K ( t,b;B _ {0} ,B _ {1} ) \leq K ( t,a;A _ {0} ,A _ {1} ) \textrm{ for all } t > 0 $$
implies that $ b \in B $ with $ \| b \| _ {B} \leq C \| a \| _ {A} $.
$ ( A _ {0} ,A _ {1} ) $ and $ ( B _ {0} ,B _ {1} ) $ are said to be relative Calderón couples if $ A $ and $ B $ are relative interpolation spaces if and only if they are relative $ K $- spaces. J. Peetre has shown (see [a6]) that if $ ( B _ {0} ,B _ {1} ) $ is any pair of weighted $ L _ \infty $ spaces, then $ ( A _ {0} ,A _ {1} ) $ and $ ( B _ {0} ,B _ {1} ) $ are relative Calderón couples for all Banach pairs $ ( A _ {0} ,A _ {1} ) $. Dually, if $ ( A _ {0} ,A _ {1} ) $ is an arbitrary pair of weighted $ L _ {1} $ spaces, then $ ( A _ {0} ,A _ {1} ) $ and $ ( B _ {0} ,B _ {1} ) $ are relative Calderón couples for all Banach pairs $ ( B _ {0} ,B _ {1} ) $ satisfying a mild "closure" condition. This latter result is another consequence of the Brudnyi–Kruglyak $ K $- divisibility theorem.
Finally, given that there are so many cases of couples whose interpolation spaces cannot be all characterized by a Calderón-style condition, one must also seek alternative ways to characterize interpolation spaces. See [a11] and [a8] for some special cases. (Cf. also [a1].)
References
| [a1] | J. Arazy, M. Cwikel, "A new characterization of the interpolation spaces between  and and 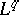 " Math. Scand. , 55 (1984) pp. 253–270 " Math. Scand. , 55 (1984) pp. 253–270 |
| [a2] | Y.A. Brudnyi, N.Ja. Krugljak, "Real interpolation functors" , North-Holland (1991) |
| [a3] | Y. Brudnyi, A. Shteinberg, "Calderón couples of Lipschitz spaces" J. Funct. Anal. , 131 (1995) pp. 459–498 |
| [a4] | A.P. Calderón, "Spaces between 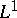 and and 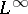 and the theorem of Marcinkiewicz" Studia Math. , 26 (1966) pp. 273–299 and the theorem of Marcinkiewicz" Studia Math. , 26 (1966) pp. 273–299 |
| [a5] | M. Cwikel, P. Nilsson, "Interpolation of weighted Banach lattices" , Memoirs , Amer. Math. Soc. (to appear) |
| [a6] | M. Cwikel, J. Peetre, "Abstract 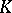 and and 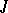 spaces" J. Math. Pures Appl. , 60 (1981) pp. 1–50 spaces" J. Math. Pures Appl. , 60 (1981) pp. 1–50 |
| [a7] | N.J. Kalton, "Calderón couples of re-arrangement invariant spaces" Studia Math. , 106 (1993) pp. 233–277 |
| [a8] | L. Maligranda, V.I. Ovchinnikov, "On interpolation between  and and  " J. Funct. Anal. , 107 (1992) pp. 343–351 " J. Funct. Anal. , 107 (1992) pp. 343–351 |
| [a9] | M. Mastyło, V.I. Ovchinnikov, "On the relation between complex and real methods of interpolation" Studia Math. (to appear) (Preprint Report 056/1996, Dept. Math. Comput. Sci. Adam Mickiewicz Univ., Poznan, 1996) |
| [a10] | B.S. Mityagin, "An interpolation theorem for modular spaces" , Proc. Conf. Interpolation Spaces and Allied Topics in Analysis, Lund, 1983 , Lecture Notes in Mathematics , 1070 , Springer (1984) pp. 10–23 (In Russian) Mat. Sbornik , 66 (1965) pp. 472–482 |
| [a11] | V.I. Ovchinnikov, "On the description of interpolation orbits in couples of 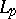 spaces when they are not described by the spaces when they are not described by the 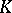 -method. Interpolation spaces and related topics" , Israel Math. Conf. Proc. Bar Ilan University , 5 , Amer. Math. Soc. (1992) pp. 187–206 -method. Interpolation spaces and related topics" , Israel Math. Conf. Proc. Bar Ilan University , 5 , Amer. Math. Soc. (1992) pp. 187–206 |
| [a12] | G. Sparr, "Interpolation of weighted 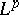 spaces" Studia Math. , 62 (1978) pp. 229–271 spaces" Studia Math. , 62 (1978) pp. 229–271 |
Calderón couples. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Calder%C3%B3n_couples&oldid=23204