CR-manifold
In 1907, H. Poincaré wrote a seminal paper, [a6], in which he showed that two real hypersurfaces in 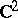 are, in general, biholomorphically inequivalent (cf. Biholomorphic mapping; Hypersurface). Later, E. Cartan [a10], [a11] found all the invariants that distinguish one real hypersurface from another. The general solution for complex dimensions greater than two was given by S.S. Chern and J. Moser [a3] and N. Tanaka [a8], [a7].
are, in general, biholomorphically inequivalent (cf. Biholomorphic mapping; Hypersurface). Later, E. Cartan [a10], [a11] found all the invariants that distinguish one real hypersurface from another. The general solution for complex dimensions greater than two was given by S.S. Chern and J. Moser [a3] and N. Tanaka [a8], [a7].
The concept of a CR-manifold (CR-structure) has been defined having in mind the geometric structure induced on a real hypersurface of 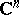 ,
, 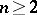 .
.
Let 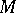 be a real differentiable manifold and
be a real differentiable manifold and 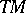 the tangent bundle of
the tangent bundle of 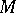 . One says that
. One says that 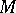 is a CR-manifold if there exists a complex subbundle
is a CR-manifold if there exists a complex subbundle 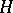 of the complexified tangent bundle
of the complexified tangent bundle 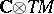 satisfying the conditions:
satisfying the conditions:
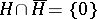 ;
;
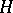 is involutive, i.e., for any complex vector fields
is involutive, i.e., for any complex vector fields 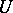 and
and 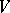 in
in 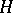 the Lie bracket
the Lie bracket 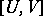 is also in
is also in 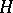 .
.
Alternatively, by using real vector bundles it can be proved (cf. [a1]) that 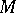 is a CR-manifold if and only if there exists an almost-complex distribution
is a CR-manifold if and only if there exists an almost-complex distribution 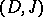 on
on 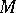 (i.e.,
(i.e., 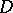 is a vector subbundle of
is a vector subbundle of 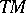 and
and 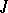 is an almost-complex structure on
is an almost-complex structure on 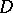 ) such that
) such that
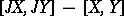 lies in
lies in 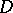 ;
;
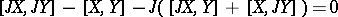 for any real vector fields
for any real vector fields 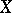 ,
, 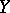 in
in 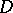 .
.
Thus the CR-structure on 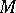 is determined either by the complex vector bundle
is determined either by the complex vector bundle 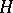 or by the almost-complex distribution
or by the almost-complex distribution 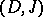 . The abbreviation CR refers to A.L. Cauchy and B. Riemann, because, for
. The abbreviation CR refers to A.L. Cauchy and B. Riemann, because, for 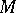 in
in 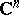 ,
, 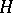 consists of the induced Cauchy–Riemann operators (cf. Cauchy–Riemann conditions).
consists of the induced Cauchy–Riemann operators (cf. Cauchy–Riemann conditions).
A 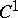 -function
-function 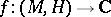 is called a CR-function if
is called a CR-function if 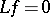 for all complex vector fields
for all complex vector fields 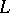 in
in 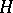 . A
. A 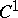 -mapping
-mapping 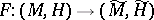 is said to be a CR-mapping if
is said to be a CR-mapping if 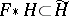 , where
, where 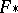 is the tangent mapping of
is the tangent mapping of 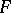 . In particular, if
. In particular, if 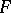 is a diffeomorphism, one says that
is a diffeomorphism, one says that 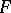 is a pseudo-conformal mapping and that
is a pseudo-conformal mapping and that 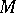 and
and 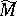 are CR-diffeomorphic or, briefly, that they are equivalent. A CR-structure on
are CR-diffeomorphic or, briefly, that they are equivalent. A CR-structure on  is said to be realizable if
is said to be realizable if 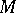 is equivalent to some real hypersurface of a complex Euclidean space.
is equivalent to some real hypersurface of a complex Euclidean space.
Let 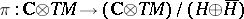 be the natural projection mapping. Then the Levi form for
be the natural projection mapping. Then the Levi form for 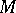 is the mapping
is the mapping
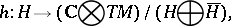 |
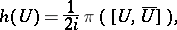 |
for any complex vector field 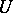 in
in 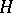 . If
. If 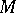 is the real hypersurface in
is the real hypersurface in 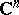 given by the equation
given by the equation 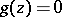 , where
, where 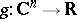 is smooth, then the Levi form for
is smooth, then the Levi form for 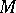 is identified with the restriction of the complex Hessian of
is identified with the restriction of the complex Hessian of 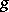 to
to 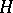 (cf. also Hessian matrix). When
(cf. also Hessian matrix). When 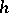 is positive- or negative-definite on
is positive- or negative-definite on 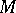 , one says that
, one says that 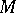 is strictly pseudo-convex.
is strictly pseudo-convex.
The differential geometry of CR-manifolds (cf. [a4]) has potential applications to both partial differential equations (cf. [a2]) and mathematical physics (cf. [a5] and [a9]).
References
| [a1] | A. Bejancu, "Geometry of CR submanifolds" , Reidel (1986) |
| [a2] | A. Boggess, "CR manifolds and tangential Cauchy–Riemann complex" , CRC (1991) |
| [a3] | S.S. Chern, J. Moser, "Real hypersurfaces in complex manifolds" Acta Math. , 133 (1974) pp. 219–271 |
| [a4] | H. Jacobowitz, "An introduction to CR structures" , Math. Surveys and Monographs , 32 , Amer. Math. Soc. (1990) |
| [a5] | R. Penrose, "Physical space-time and non-realizable CR structures" , Proc. Symp. Pure Math. , 39 , Amer. Math. Soc. (1983) pp. 401–422 |
| [a6] | H. Poincaré, "Les functions analytiques de deux variables et la représentation conforme" Rend. Circ. Mat. Palermo , 23 (1907) pp. 185–220 |
| [a7] | N. Tanaka, "On the pseudo-conformal geometry of hypersurfaces of the space of  complex variables" J. Math. Soc. Japan , 14 (1962) pp. 397–429 complex variables" J. Math. Soc. Japan , 14 (1962) pp. 397–429 |
| [a8] | N. Tanaka, "On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections" Japan J. Math. (N.S.) , 2 (1976) pp. 131–190 |
| [a9] | J.R. Wells, Jr., "Complex manifolds and mathematical physics" Bull. Amer. Math. Soc. (N.S.) , 1 (1979) pp. 296–336 |
| [a10] | É. Cartan, "Sur l'équivalence pseudo-conforme des hypersurfaces de l'espace de deux variables complexes I." Ann. Mathém. , 11 (1932) pp. 17–90 |
| [a11] | É. Cartan, "Sur l'équivalence pseudo-conforme des hypersurfaces de l'espace de deux variable complexes II." Ann. Scuola Norm. Sup. Pisa , 1 (1932) pp. 333–354 |
CR-manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=CR-manifold&oldid=11362