Busemann function
A concept of function which measures the distance to a point at infinity. Let  be a Riemannian manifold. The Riemannian metric induces a distance function
be a Riemannian manifold. The Riemannian metric induces a distance function  on
on  . Let
. Let  be a ray in
be a ray in  , i.e., a unit-speed geodesic line
, i.e., a unit-speed geodesic line  such that
such that 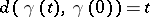 for all
for all  . The Busemann function
. The Busemann function  with respect to
with respect to 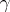 is defined by
is defined by
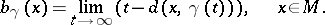 |
Since 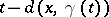 is bounded above by
is bounded above by 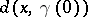 and is monotone non-decreasing in
and is monotone non-decreasing in 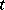 , the limit always exits. It follows that
, the limit always exits. It follows that 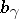 is a Lipschitz function with Lipschitz constant
is a Lipschitz function with Lipschitz constant 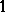 . The level surfaces
. The level surfaces 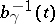 of a Busemann function are called horospheres. Busemann functions can also be defined on intrinsic (or length) metric spaces, in the same manner. Actually, H. Busemann [a2] first introduced them on so-called
of a Busemann function are called horospheres. Busemann functions can also be defined on intrinsic (or length) metric spaces, in the same manner. Actually, H. Busemann [a2] first introduced them on so-called 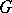 -spaces and used them to state the parallel axiom on straight
-spaces and used them to state the parallel axiom on straight 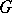 -spaces (cf. also Closed geodesic).
-spaces (cf. also Closed geodesic).
If 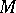 has non-negative sectional curvature,
has non-negative sectional curvature, 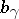 is convex, see [a3]. If
is convex, see [a3]. If 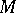 has non-negative Ricci curvature,
has non-negative Ricci curvature, 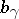 is a subharmonic function, see [a4]. If
is a subharmonic function, see [a4]. If 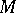 is a Kähler manifold with non-negative holomorphic bisectional curvature,
is a Kähler manifold with non-negative holomorphic bisectional curvature, 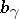 is a plurisubharmonic function, see [a7]. If
is a plurisubharmonic function, see [a7]. If 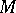 is a Hadamard manifold,
is a Hadamard manifold, 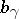 is a
is a 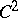 concave function, see [a9], [a2], and, moreover, the horospheres are
concave function, see [a9], [a2], and, moreover, the horospheres are 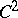 -hypersurfaces, see [a9]. On the Poincaré model
-hypersurfaces, see [a9]. On the Poincaré model  of the hyperbolic space, the horospheres coincide with the Euclidean spheres in
of the hyperbolic space, the horospheres coincide with the Euclidean spheres in 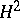 which are tangent to the sphere at infinity. On Hadamard manifolds, it is more customary to call
which are tangent to the sphere at infinity. On Hadamard manifolds, it is more customary to call 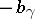 the Busemann function instead of
the Busemann function instead of 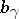 .
.
More recently, M. Gromov [a1] introduced a generalization of the concept of Busemann function called the horofunction. Let 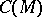 be the set of continuous functions on
be the set of continuous functions on 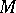 and let
and let 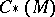 the quotient space of
the quotient space of 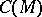 modulo the constant functions. Use the topology on
modulo the constant functions. Use the topology on 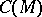 induced from the uniform convergence on compact sets and its quotient topology on
induced from the uniform convergence on compact sets and its quotient topology on 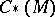 . The embedding of
. The embedding of 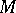 into
into  defined by
defined by 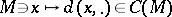 induces an embedding
induces an embedding 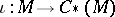 . The closure of the image
. The closure of the image 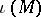 is a compactification of
is a compactification of  (cf. also Compactification). According to [a1], [a8], a horofunction is defined to be a class (or an element of a class) in the topological boundary
(cf. also Compactification). According to [a1], [a8], a horofunction is defined to be a class (or an element of a class) in the topological boundary 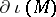 of
of 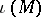 in
in 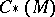 . Any Busemann function is a horofunction. For Hadamard manifolds, any horofunction can be represented as some Busemann function, see [a1]. However, this is not necessarily true for non-Hadamard manifolds. Horofunctions have been defined not only for Riemannian manifolds but also for complete locally compact metric spaces.
. Any Busemann function is a horofunction. For Hadamard manifolds, any horofunction can be represented as some Busemann function, see [a1]. However, this is not necessarily true for non-Hadamard manifolds. Horofunctions have been defined not only for Riemannian manifolds but also for complete locally compact metric spaces.
Let 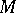 be a complete non-compact Riemannian manifold with non-negative sectional curvature, and for
be a complete non-compact Riemannian manifold with non-negative sectional curvature, and for 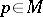 , let
, let 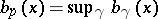 ,
,  , where
, where 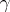 runs over all rays emanating from
runs over all rays emanating from 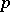 . Then,
. Then, 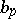 is a convex exhaustion function, see [a3], that is, a function
is a convex exhaustion function, see [a3], that is, a function 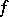 on
on 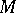 such that
such that 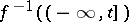 is compact for any
is compact for any 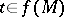 . The function
. The function 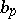 plays an important role in the first step of the Cheeger–Gromoll structure theory for
plays an important role in the first step of the Cheeger–Gromoll structure theory for 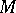 , see [a3]. Any Kähler manifold admitting a strictly plurisubharmonic exhaustion function is a Stein manifold, see [a5]. This, together with the use of Busemann functions or
, see [a3]. Any Kähler manifold admitting a strictly plurisubharmonic exhaustion function is a Stein manifold, see [a5]. This, together with the use of Busemann functions or 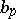 , yields various sufficient conditions for a Kähler manifold to be Stein; see, for example, [a7], [a17]. Some results for the exhaustion property of Busemann functions are known, see [a14], [a15], [a12], [a13]. For a generalization of the notion of a horofunction and of
, yields various sufficient conditions for a Kähler manifold to be Stein; see, for example, [a7], [a17]. Some results for the exhaustion property of Busemann functions are known, see [a14], [a15], [a12], [a13]. For a generalization of the notion of a horofunction and of 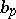 , see [a18]. A general reference for Busemann function and its related topics is [a16].
, see [a18]. A general reference for Busemann function and its related topics is [a16].
References
| [a1] | W. Ballmann, M. Gromov, V. Schroeder, "Manifolds of nonpositive curvature" , Progr. Math. , 61 , Birkhäuser (1985) |
| [a2] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
| [a3] | J. Cheeger, D. Gromoll, "On the structure of complete manifolds of nonnegative curvature" Ann. of Math. (2) , 96 (1972) pp. 413–443 |
| [a4] | J. Cheeger, D. Gromoll, "The splitting theorem for manifolds of nonnegative Ricci curvature" J. Diff. Geom. , 6 (1971/72) pp. 119–128 |
| [a5] | F. Docquier, H. Grauert, "Leisches Problem und Rungescher Satz für Teilgebiete Steinscher Mannigfaltigkeiten" Math. Ann. , 140 (1960) pp. 94–123 |
| [a6] | P. Eberlein, B. O'Neill, "Visibility manifolds" Pacific J. Math. , 46 (1973) pp. 45–109 |
| [a7] | R.E. Greene, H. Wu, "On Kähler manifolds of positive bisectional curvature and a theorem of Hartogs" Abh. Math. Sem. Univ. Hamburg , 47 (1978) pp. 171–185 (Special issue dedicated to the seventieth birthday of Erich Käler) |
| [a8] | M. Gromov, "Structures métriques pour les variétés riemanniennes" , Textes Mathématiques [Mathematical Texts] , 1 , CEDIC (1981) (Edited by J. Lafontaine and P. Pansu) |
| [a9] | E. Heintze, H.-C. Im Hof, "Geometry of horospheres" J. Diff. Geom. , 12 : 4 (1977) pp. 481–491 (1978) |
| [a10] | N. Innami, "On the terminal points of co-rays and rays" Arch. Math. (Basel) , 45 : 5 (1985) pp. 468–470 |
| [a11] | N. Innami, "Differentiability of Busemann functions and total excess" Math. Z. , 180 : 2 (1982) pp. 235–247 |
| [a12] | A. Kasue, "A compactification of a manifold with asymptotically nonnegative curvature" Ann. Sci. Ecole Norm. Sup. 4 , 21 : 4 (1988) pp. 593–622 |
| [a13] | Z. Shen, "On complete manifolds of nonnegative 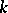 th-Ricci curvature" Trans. Amer. Math. Soc. , 338 : 1 (1993) pp. 289–310 th-Ricci curvature" Trans. Amer. Math. Soc. , 338 : 1 (1993) pp. 289–310 |
| [a14] | K. Shiohama, "Busemann functions and total curvature" Invent. Math. , 53 : 3 (1979) pp. 281–297 |
| [a15] | K. Shiohama, "The role of total curvature on complete noncompact Riemannian  -manifolds" Illinois J. Math. , 28 : 4 (1984) pp. 597–620 -manifolds" Illinois J. Math. , 28 : 4 (1984) pp. 597–620 |
| [a16] | K. Shiohama, "Topology of complete noncompact manifolds" , Geometry of Geodesics and Related Topics (Tokyo, 1982) , Adv. Stud. Pure Math. , 3 , North-Holland (1984) pp. 423–450 |
| [a17] | Y.T. Siu, S.T. Yau, "Complete Kähler manifolds with nonpositive curvature of faster than quadratic decay" Ann. of Math. (2) , 105 : 2 (1977) pp. 225–264 |
| [a18] | H. Wu, "An elementary method in the study of nonnegative curvature" Acta Math. , 142 : 1–2 (1979) pp. 57–78 |
Busemann function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Busemann_function&oldid=13719