Burnside Lemma
Burnside Theorem
The famous theorem which is often referred to as "Burnside's Lemma" or "Burnside's Theorem" states that when a finite group  acts on a set
acts on a set  , the number
, the number  of orbits is the average number of fixed points of elements of
of orbits is the average number of fixed points of elements of 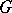 , that is,
, that is, 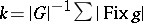 , where
, where 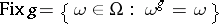 and the sum is over all
and the sum is over all 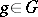 . It is widely used in applications of group theory to combinatorics; in particular, it is the basis of the theory of combinatorial enumeration invented by J.H. Redfield [a7] and G. Pólya [a6]. Proofs are to be found in many textbooks on combinatorics and many elementary books on group theory (see, for example, [a5], Chap. 9).
. It is widely used in applications of group theory to combinatorics; in particular, it is the basis of the theory of combinatorial enumeration invented by J.H. Redfield [a7] and G. Pólya [a6]. Proofs are to be found in many textbooks on combinatorics and many elementary books on group theory (see, for example, [a5], Chap. 9).
The name refers to William Burnside (1852–1927), not to W.S. Burnside (1839–1920). There are several lemmas and theorems in group theory and representation theory to which the name of William Burnside is correctly attached (for example: Burnside's transfer theorem; Burnside's  -theorem; Burnside's basis theorem for
-theorem; Burnside's basis theorem for 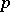 -groups). In this case, however, it is a misattribution dating from about 1960 (see [a4], [a8]). Although the result can be traced back to some work of A.L. Cauchy in 1845, in the above form it was published in 1887 by G. Frobenius [a3]. It appears in the 1897 edition of Burnside's classic [a1] with appropriate reference to Frobenius, but in the second edition [a2] the attribution has been mysteriously dropped, and this is almost certainly one reason for later confusion. Because of its origins the theorem has been referred to as the Cauchy–Frobenius theorem and also, on rare occasions, as Not Burnside's Lemma.
-groups). In this case, however, it is a misattribution dating from about 1960 (see [a4], [a8]). Although the result can be traced back to some work of A.L. Cauchy in 1845, in the above form it was published in 1887 by G. Frobenius [a3]. It appears in the 1897 edition of Burnside's classic [a1] with appropriate reference to Frobenius, but in the second edition [a2] the attribution has been mysteriously dropped, and this is almost certainly one reason for later confusion. Because of its origins the theorem has been referred to as the Cauchy–Frobenius theorem and also, on rare occasions, as Not Burnside's Lemma.
References
| [a1] | W. Burnside, "Theory of groups of finite order" , Cambridge Univ. Press (1897) |
| [a2] | W. Burnside, "Theory of groups of finite order" , Cambridge Univ. Press (1911) (Reprinted: Dover, 1955) |
| [a3] | G. Frobenius, "Über die Congruenz nach einem aus zwei endlichen Gruppen gebildeten Doppelmodul" J. Reine Angew. Math. , 101 (1887) pp. 273–299 (Also: Gesammelte Abh. II (1968), Springer, 304-330) |
| [a4] | Peter M. Neumann, "A lemma that is not Burnside's" Math. Scientist , 4 (1979) pp. 133–141 |
| [a5] | Peter M. Neumann, G.A. Stoy, E.C. Thompson, "Groups and geometry" , Clarendon Press (1994) |
| [a6] | G. Pólya, "Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen" Acta Math. , 68 (1937) pp. 145–254 |
| [a7] | J.H. Redfield, "The theory of group-reduced distributions" Amer. J. Math. , 49 (1927) pp. 433–455 |
| [a8] | E.M. Wright, "Burnside's lemma: a historical note" J. Combin. Th. B , 30 (1981) pp. 89–90 |
Burnside Lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Burnside_Lemma&oldid=14747