Budan-Fourier theorem
From Encyclopedia of Mathematics
The number of roots of an algebraic equation
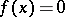 |
comprised in an interval 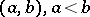 , is equal to or is smaller, by an even number, than
, is equal to or is smaller, by an even number, than 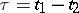 , where
, where 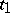 is the number of changes in sign in the series of derivatives of the polynomial
is the number of changes in sign in the series of derivatives of the polynomial  at the point
at the point  , i.e. in the series
, i.e. in the series
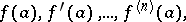 |
while 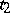 is the number of changes in sign in this series at the point
is the number of changes in sign in this series at the point 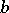 . Each multiple root is counted according to its multiplicity. Established by F. Budan (1822) and J. Fourier (1820).
. Each multiple root is counted according to its multiplicity. Established by F. Budan (1822) and J. Fourier (1820).
References
| [1] | , Encyclopaedia of elementary mathematics , 2. Algebra , Moscow-Leningrad (1951) pp. 331 (In Russian) |
Comments
An application of the Budan–Fourier theorem in numerical analysis may be found in [a1], where it is used in the interpolation by spline functions.
References
| [a1] | C. de Boor, I.J. Schoenberg, "Cardinal interpolation and spline functions VIII. The Budan–Fourier theorem for splines and applications." K. Bohmer (ed.) G. Meinardus (ed.) W. Schempp (ed.) , Spline functions , Lect. notes in math. , 501 , Springer (1976) |
| [a2] | A.S. Householder, "Unique triangularization of a nonsymmetric matrix" J. Assoc. Comp. Mach. , 5 (1958) pp. 339–342 |
How to Cite This Entry:
Budan-Fourier theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Budan-Fourier_theorem&oldid=15303
Budan-Fourier theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Budan-Fourier_theorem&oldid=15303
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article