Brun sieve
A sieve method in elementary number theory, proposed by V. Brun [1]; it is an extension of the sieve of Eratosthenes (cf. Eratosthenes, sieve of). The method of Brun's sieve may be described as follows. Out of a sequence of natural numbers 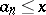 the numbers with small prime divisors are eliminated ( "sieved out" ) leaving behind prime and almost-prime numbers (cf. Almost-prime number) with only large prime divisors. Let
the numbers with small prime divisors are eliminated ( "sieved out" ) leaving behind prime and almost-prime numbers (cf. Almost-prime number) with only large prime divisors. Let 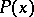 be the amount of these numbers. It can be shown that
be the amount of these numbers. It can be shown that 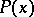 is included between two sums with a relatively-small number of summands, which may be estimated from above and from below. Thus, it is possible to evaluate from above the number of twins in a given interval. Brun's sieve is employed in additive number theory. Brun used his sieve to prove that all large even numbers
is included between two sums with a relatively-small number of summands, which may be estimated from above and from below. Thus, it is possible to evaluate from above the number of twins in a given interval. Brun's sieve is employed in additive number theory. Brun used his sieve to prove that all large even numbers 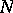 can be represented in the form
can be represented in the form 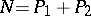 , where
, where 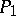 and
and 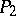 contain at most 9 prime factors.
contain at most 9 prime factors.
References
| [1] | V. Brun, "Le crible d'Eratosthène et le théorème de Goldbach" C.R. Acad. Sci. Paris Sér. I Math. , 168 : 11 (1919) pp. 544–546 |
| [2] | A.O. Gel'fond, Yu.V. Linnik, "Elementary methods in the analytic theory of numbers" , M.I.T. (1966) (Translated from Russian) |
| [3] | E. Trost, "Primzahlen" , Birkhäuser (1953) |
Comments
References
| [a1] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
Brun sieve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brun_sieve&oldid=13625