Bruhat decomposition
A representation of a connected algebraic reductive group 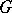 as the union of double cosets of a Borel subgroup, parametrized by the Weyl group of
as the union of double cosets of a Borel subgroup, parametrized by the Weyl group of 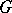 . More exactly, let
. More exactly, let 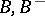 be opposite Borel subgroups of a reductive group
be opposite Borel subgroups of a reductive group 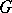 ; let
; let 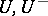 be the respective unipotent parts of
be the respective unipotent parts of 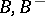 (cf. Linear algebraic group) and let
(cf. Linear algebraic group) and let 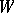 be the Weyl group of
be the Weyl group of 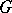 . In what follows
. In what follows 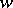 denotes both an element of
denotes both an element of 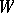 and its representative in the normalizer of the torus
and its representative in the normalizer of the torus  , since the construction presented below is independent of the representative chosen. The group
, since the construction presented below is independent of the representative chosen. The group 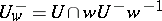 will then be considered for each
will then be considered for each 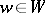 . The group
. The group 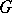 is then representable as the union of the non-intersecting double cosets
is then representable as the union of the non-intersecting double cosets 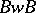 (
(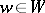 ), and the morphism
), and the morphism 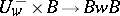
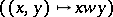 is an isomorphism of algebraic varieties. An even more precise formulation of the Bruhat decomposition will yield a cellular decomposition of the projective variety
is an isomorphism of algebraic varieties. An even more precise formulation of the Bruhat decomposition will yield a cellular decomposition of the projective variety 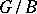 . Namely, if
. Namely, if 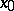 is a fixed (with respect to the left shifts by elements from
is a fixed (with respect to the left shifts by elements from 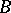 ) point of
) point of 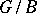 (such a point always exists, cf. Borel fixed-point theorem),
(such a point always exists, cf. Borel fixed-point theorem), 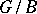 will be the union of non-intersecting
will be the union of non-intersecting 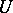 -orbits of the type
-orbits of the type  ,
, 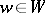 (cf. Algebraic group of transformations), and the morphism
(cf. Algebraic group of transformations), and the morphism 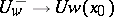
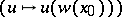 is an isomorphism of algebraic varieties. All groups
is an isomorphism of algebraic varieties. All groups 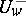 , being varieties, are isomorphic to an affine space; if the ground field is the field of complex numbers, then each of the above
, being varieties, are isomorphic to an affine space; if the ground field is the field of complex numbers, then each of the above 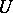 -orbits is a cell in the sense of algebraic topology so that the homology of
-orbits is a cell in the sense of algebraic topology so that the homology of 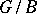 can be calculated. The existence of a Bruhat decomposition for a number of classical groups was established in 1956 by F. Bruhat, and was proved in the general case by C. Chevalley [3]. A. Borel and J. Tits generalized the construction of Bruhat decompositions to the groups
can be calculated. The existence of a Bruhat decomposition for a number of classical groups was established in 1956 by F. Bruhat, and was proved in the general case by C. Chevalley [3]. A. Borel and J. Tits generalized the construction of Bruhat decompositions to the groups 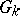 of
of 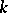 -points of a
-points of a 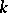 -defined algebraic group [2], the role of Borel subgroups being played by minimal parabolic
-defined algebraic group [2], the role of Borel subgroups being played by minimal parabolic 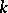 -subgroups, the role of the groups
-subgroups, the role of the groups 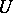 by their unipotent radicals; the Weyl
by their unipotent radicals; the Weyl 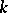 -group
-group 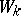 or the relative Weyl group was considered instead of
or the relative Weyl group was considered instead of 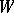 .
.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 |
| [3] | C. Chevalley, "Classification des groupes de Lie algébriques" , 2 , Ecole Norm. Sup. (1958) |
Bruhat decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bruhat_decomposition&oldid=17813