Difference between revisions of "Brown-Peterson spectrum"
Ulf Rehmann (talk | contribs) m (moved Brown–Peterson spectrum to Brown-Peterson spectrum: ascii title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1109301.png | ||
| + | $#A+1 = 16 n = 3 | ||
| + | $#C+1 = 16 : ~/encyclopedia/old_files/data/B110/B.1100930 Brown\ANDPeterson spectrum | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | By the Pontryagin–Thom theorem, there is a ring spectrum $ MU $( | |
| + | cf. [[Spectrum of a ring|Spectrum of a ring]]) whose [[Homotopy|homotopy]] is isomorphic to the graded ring of bordism classes of closed smooth manifolds with a complex structure on their stable normal bundles (cf. also [[Cobordism|Cobordism]]). E.H. Brown and F.P. Peterson [[#References|[a1]]] showed that, when localized at a prime $ p $, | ||
| + | the spectrum $ MU $ | ||
| + | is homotopy equivalent to the wedge of various suspensions (cf. also [[Suspension|Suspension]]) of a ring spectrum $ BP $, | ||
| + | the Brown–Peterson spectrum. The homotopy of this spectrum is the polynomial algebra | ||
| − | + | $$ | |
| + | \pi _ {*} BP = \mathbf Z _ {( p ) } [ v _ {1} \dots v _ {n} , \dots ] , | ||
| + | $$ | ||
| − | + | where the degree of $ v _ {n} $ | |
| + | is $ 2 ( p ^ {n} - 1 ) $. | ||
| + | As a module over the [[Steenrod algebra|Steenrod algebra]], | ||
| − | An introduction to the study of | + | $$ |
| + | H _ {*} ( BP; \mathbf Z/p ) \simeq \left \{ | ||
| + | \begin{array}{l} | ||
| + | {\mathbf Z/2 [ \xi _ {1} ^ {2} \dots \xi _ {n} ^ {2} , \dots ] , \ p = 2, } \\ | ||
| + | {\mathbf Z/p [ \xi _ {1} \dots \xi _ {n} , \dots ] , \ p \textrm{ odd } . } | ||
| + | \end{array} | ||
| + | \right . | ||
| + | $$ | ||
| + | |||
| + | Four properties of $ BP $ | ||
| + | have made it one of the most useful spectra in homotopy theory. First, D. Quillen [[#References|[a5]]] determined the structure of its ring of operations. Second, A. Liulevicius [[#References|[a3]]] and M. Hazewinkel [[#References|[a2]]] constructed polynomial generators of $ \pi _ {*} BP $ | ||
| + | with good properties. Third, the Baas–Sullivan construction can be used to construct simple spectra from $ BP $ | ||
| + | with very nice properties. The most notable of these spectra are the Morava $ K $- | ||
| + | theories $ K ( n ) $, | ||
| + | which are central in the statement of the periodicity theorem. (See [[#References|[a7]]] for an account of the nilpotence and periodicity theorems.) Fourth, S.P. Novikov [[#References|[a4]]] constructed the Adams–Novikov [[Spectral sequence|spectral sequence]], which uses knowledge of the Brown–Peterson homology of a spectrum $ X $ | ||
| + | to compute the homotopy of $ X $. | ||
| + | (See [[#References|[a6]]] for a survey of how the Adams–Novikov spectral sequence gives information on the stable homotopy groups of spheres.) | ||
| + | |||
| + | An introduction to the study of $ BP $ | ||
| + | is given in [[#References|[a8]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.H. Brown, F.P. Peterson, "A spectrum whose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110930/b11093018.png" />-homology is the algebra of reduced <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110930/b11093019.png" />th powers" ''Topology'' , '''5''' (1966) pp. 149–154</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Hazewinkel, "Constructing formal groups III. Applications to complex cobordism and Brown–Peterson cohomology" ''J. Pure Appl. Algebra'' , '''10''' (1977/78) pp. 1–18</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Liulevicius, "On the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110930/b11093020.png" />" , ''Lecture Notes in Mathematics'' , '''249''' , Springer (1971) pp. 47–53</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.P. Novikov, "The methods of algebraic topology from the viewpoint of cobordism theories" ''Math. USSR Izv.'' (1967) pp. 827–913 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''31''' (1967) pp. 855–951</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Quillen, "On the formal group laws of unoriented and complex cobordism theory" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 1293–1298</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D.C. Ravenel, "Complex cobordism and stable homotopy groups of spheres" , ''Pure and Applied Mathematics'' , '''121''' , Acad. Press (1986)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D.C. Ravenel, "Nilpotence and periodicity in stable homotopy theory" , ''Annals of Math. Stud.'' , '''128''' , Princeton Univ. Press (1992)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> W.S. Wilson, "Brown–Peterson homology, an introduction and sampler" , ''Regional Conf. Ser. Math.'' , '''48''' , Amer. Math. Soc. (1982)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.H. Brown, F.P. Peterson, "A spectrum whose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110930/b11093018.png" />-homology is the algebra of reduced <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110930/b11093019.png" />th powers" ''Topology'' , '''5''' (1966) pp. 149–154</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Hazewinkel, "Constructing formal groups III. Applications to complex cobordism and Brown–Peterson cohomology" ''J. Pure Appl. Algebra'' , '''10''' (1977/78) pp. 1–18</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Liulevicius, "On the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110930/b11093020.png" />" , ''Lecture Notes in Mathematics'' , '''249''' , Springer (1971) pp. 47–53</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S.P. Novikov, "The methods of algebraic topology from the viewpoint of cobordism theories" ''Math. USSR Izv.'' (1967) pp. 827–913 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''31''' (1967) pp. 855–951</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Quillen, "On the formal group laws of unoriented and complex cobordism theory" ''Bull. Amer. Math. Soc.'' , '''75''' (1969) pp. 1293–1298</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D.C. Ravenel, "Complex cobordism and stable homotopy groups of spheres" , ''Pure and Applied Mathematics'' , '''121''' , Acad. Press (1986)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D.C. Ravenel, "Nilpotence and periodicity in stable homotopy theory" , ''Annals of Math. Stud.'' , '''128''' , Princeton Univ. Press (1992)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> W.S. Wilson, "Brown–Peterson homology, an introduction and sampler" , ''Regional Conf. Ser. Math.'' , '''48''' , Amer. Math. Soc. (1982)</TD></TR></table> | ||
Revision as of 06:29, 30 May 2020
By the Pontryagin–Thom theorem, there is a ring spectrum $ MU $(
cf. Spectrum of a ring) whose homotopy is isomorphic to the graded ring of bordism classes of closed smooth manifolds with a complex structure on their stable normal bundles (cf. also Cobordism). E.H. Brown and F.P. Peterson [a1] showed that, when localized at a prime $ p $,
the spectrum $ MU $
is homotopy equivalent to the wedge of various suspensions (cf. also Suspension) of a ring spectrum $ BP $,
the Brown–Peterson spectrum. The homotopy of this spectrum is the polynomial algebra
$$ \pi _ {*} BP = \mathbf Z _ {( p ) } [ v _ {1} \dots v _ {n} , \dots ] , $$
where the degree of $ v _ {n} $ is $ 2 ( p ^ {n} - 1 ) $. As a module over the Steenrod algebra,
$$ H _ {*} ( BP; \mathbf Z/p ) \simeq \left \{ \begin{array}{l} {\mathbf Z/2 [ \xi _ {1} ^ {2} \dots \xi _ {n} ^ {2} , \dots ] , \ p = 2, } \\ {\mathbf Z/p [ \xi _ {1} \dots \xi _ {n} , \dots ] , \ p \textrm{ odd } . } \end{array} \right . $$
Four properties of $ BP $ have made it one of the most useful spectra in homotopy theory. First, D. Quillen [a5] determined the structure of its ring of operations. Second, A. Liulevicius [a3] and M. Hazewinkel [a2] constructed polynomial generators of $ \pi _ {*} BP $ with good properties. Third, the Baas–Sullivan construction can be used to construct simple spectra from $ BP $ with very nice properties. The most notable of these spectra are the Morava $ K $- theories $ K ( n ) $, which are central in the statement of the periodicity theorem. (See [a7] for an account of the nilpotence and periodicity theorems.) Fourth, S.P. Novikov [a4] constructed the Adams–Novikov spectral sequence, which uses knowledge of the Brown–Peterson homology of a spectrum $ X $ to compute the homotopy of $ X $. (See [a6] for a survey of how the Adams–Novikov spectral sequence gives information on the stable homotopy groups of spheres.)
An introduction to the study of $ BP $ is given in [a8].
References
| [a1] | E.H. Brown, F.P. Peterson, "A spectrum whose 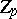 -homology is the algebra of reduced -homology is the algebra of reduced 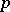 th powers" Topology , 5 (1966) pp. 149–154 th powers" Topology , 5 (1966) pp. 149–154 |
| [a2] | M. Hazewinkel, "Constructing formal groups III. Applications to complex cobordism and Brown–Peterson cohomology" J. Pure Appl. Algebra , 10 (1977/78) pp. 1–18 |
| [a3] | A. Liulevicius, "On the algebra 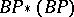 " , Lecture Notes in Mathematics , 249 , Springer (1971) pp. 47–53 " , Lecture Notes in Mathematics , 249 , Springer (1971) pp. 47–53 |
| [a4] | S.P. Novikov, "The methods of algebraic topology from the viewpoint of cobordism theories" Math. USSR Izv. (1967) pp. 827–913 Izv. Akad. Nauk SSSR Ser. Mat. , 31 (1967) pp. 855–951 |
| [a5] | D. Quillen, "On the formal group laws of unoriented and complex cobordism theory" Bull. Amer. Math. Soc. , 75 (1969) pp. 1293–1298 |
| [a6] | D.C. Ravenel, "Complex cobordism and stable homotopy groups of spheres" , Pure and Applied Mathematics , 121 , Acad. Press (1986) |
| [a7] | D.C. Ravenel, "Nilpotence and periodicity in stable homotopy theory" , Annals of Math. Stud. , 128 , Princeton Univ. Press (1992) |
| [a8] | W.S. Wilson, "Brown–Peterson homology, an introduction and sampler" , Regional Conf. Ser. Math. , 48 , Amer. Math. Soc. (1982) |
Brown-Peterson spectrum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brown-Peterson_spectrum&oldid=22199