Brouwer lattice
Brouwer structure, Brouwer algebra
A distributive lattice in which for each pair of elements  there exists an element, called the pseudo-difference (frequently denoted by
there exists an element, called the pseudo-difference (frequently denoted by  ), which is the smallest element
), which is the smallest element  possessing the property
possessing the property  . An equivalent description of a Brouwer lattice is as a variety of universal algebras (cf. Universal algebra) with three binary operations
. An equivalent description of a Brouwer lattice is as a variety of universal algebras (cf. Universal algebra) with three binary operations  ,
,  and
and  , which satisfies certain axioms. The term "Brouwer algebra" was introduced in recognition of the connection between Brouwer lattices and Brouwer's intuitionistic logic. Instead of Brouwer lattices the so-called pseudo-Boolean algebras are often employed, the theory of which is dual to that of Brouwer lattices. Any Brouwer lattice can be converted to a pseudo-Boolean algebra by the introduction of a new order
, which satisfies certain axioms. The term "Brouwer algebra" was introduced in recognition of the connection between Brouwer lattices and Brouwer's intuitionistic logic. Instead of Brouwer lattices the so-called pseudo-Boolean algebras are often employed, the theory of which is dual to that of Brouwer lattices. Any Brouwer lattice can be converted to a pseudo-Boolean algebra by the introduction of a new order  , and of new unions and intersections according to the formulas
, and of new unions and intersections according to the formulas
 |
and the operation of relative pseudo-complementation 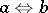 which corresponds to the pseudo-difference
which corresponds to the pseudo-difference  . Conversely, any pseudo-Boolean algebra can be regarded as a Brouwer lattice. The term "Brouwer lattice" is sometimes used to denote a pseudo-Boolean algebra (see, for instance, [2]).
. Conversely, any pseudo-Boolean algebra can be regarded as a Brouwer lattice. The term "Brouwer lattice" is sometimes used to denote a pseudo-Boolean algebra (see, for instance, [2]).
References
| [1] | J.C.C. McKinsey, A. Tarski, "The algebra of topology" Ann. of Math. (2) , 45 : 1 (1944) pp. 141–191 |
| [2] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1967) |
Comments
In Western literature pseudo-Boolean algebras are more commonly called Heyting algebras. Complete Heyting algebras (often called frames or locales) have been extensively studied on account of their connections with topology: the lattice of open sets of any topological space is a locale, and locales can in some respects be considered as generalized topological spaces. See [a1], [a2], [a3].
References
| [a1] | M.P. Fourman, D.S. Scott, "Sheaves and logic" M.P. Fourman (ed.) C.J. Mulvey (ed.) D.S. Scott (ed.) , Applications of sheaves , Lect. notes in math. , 753 , Springer (1979) pp. 302–401 |
| [a2] | P.T. Johnstone, "Stone spaces" , Cambridge Univ. Press (1983) |
| [a3] | H. Simmons, "A framework for topology" , Logic colloquium '77 , Studies in logic and foundations of math. , 96 , North-Holland (1978) pp. 239–251 |
Brouwer lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brouwer_lattice&oldid=13466