Brocard point
The first (or positive) Brocard point of a plane triangle 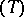 with vertices
with vertices 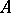 ,
, 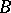 ,
, 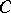 is the interior point
is the interior point  of
of 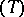 for which the three angles
for which the three angles 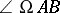 ,
, 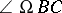 ,
,  are equal. Their common value
are equal. Their common value 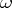 is the Brocard angle of
is the Brocard angle of 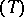 .
.
The second (or negative) Brocard point of 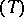 is the interior point
is the interior point 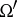 for which
for which 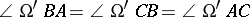 . Their common value is again
. Their common value is again 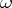 . The Brocard angle satisfies
. The Brocard angle satisfies 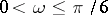 . The two Brocard points are isogonal conjugates (cf. Isogonal); they coincide if
. The two Brocard points are isogonal conjugates (cf. Isogonal); they coincide if 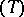 is equilateral, in which case
is equilateral, in which case 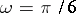 .
.
The Brocard configuration (for an extensive account see [a6]), named after H. Brocard who first published about it around 1875, belongs to triangle geometry, a subbranch of Euclidean geometry that thrived in the last quarter of the nineteenth century to fade away again in the first quarter of the twentieth century. A brief historical account is given in [a5].
Although his name is generally associated with the points  and
and 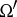 , Brocard was not the first person to investigate their properties; in 1816, long before Brocard wrote about them, they were mentioned by A.L. Crelle in [a4] (see also [a8] and [a11]). Information on Brocard's life can be found in [a7].
, Brocard was not the first person to investigate their properties; in 1816, long before Brocard wrote about them, they were mentioned by A.L. Crelle in [a4] (see also [a8] and [a11]). Information on Brocard's life can be found in [a7].
The Brocard points and Brocard angle have many remarkable properties. Some characteristics of the Brocard configuration are given below.
Let 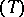 be an arbitrary plane triangle with vertices
be an arbitrary plane triangle with vertices 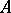 ,
, 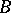 ,
, 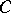 and angles
and angles 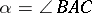 ,
, 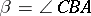 ,
, 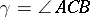 . If
. If 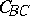 denotes the circle that is tangent to the line
denotes the circle that is tangent to the line 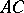 at
at  and passes through the vertices
and passes through the vertices 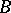 and
and 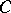 , then
, then 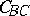 also passes through
also passes through  . Similarly for the circles
. Similarly for the circles 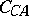 and
and 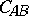 . So the three circles
. So the three circles 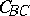 ,
, 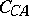 ,
, 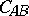 intersect in the first Brocard point
intersect in the first Brocard point  . Analogously, the circle
. Analogously, the circle 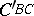 that passes through
that passes through 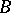 and
and 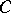 and is tangent to the line
and is tangent to the line 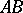 at
at 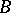 , meets the circles
, meets the circles 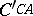 and
and 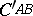 in the second Brocard point
in the second Brocard point 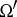 . Further, the circumcentre
. Further, the circumcentre 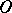 of
of 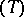 and the two Brocard points are vertices of a isosceles triangle for which
and the two Brocard points are vertices of a isosceles triangle for which 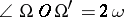 . The lengths of the sides of this triangle can be expressed in terms of the radius
. The lengths of the sides of this triangle can be expressed in terms of the radius 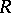 of the circumcircle of
of the circumcircle of 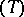 , and the Brocard angle
, and the Brocard angle 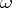 :
:
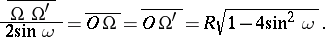 |
The Brocard circle is the circle passing through the two Brocard points and 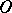 . The Lemoine point
. The Lemoine point 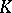 of
of 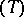 , named after E. Lemoine, is a distinguished point of this circle, and the length of the line segment
, named after E. Lemoine, is a distinguished point of this circle, and the length of the line segment
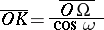 |
gives the diameter of the Brocard circle.
The Brocard angle 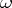 is related to the three angles
is related to the three angles 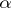 ,
, 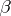 ,
, 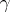 by the following trigonometric identities:
by the following trigonometric identities:
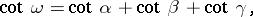 |
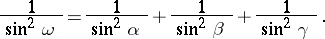 |
Due to a remarkable conjecture by P. Yff in 1963 (see [a14]), modest interest in the Brocard configuration arose again during the 1960s, 1970s and 1980s. This conjecture, known as Yff's inequality,
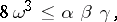 |
is unusual in the sense that it contains the angles proper instead of their trigonometric function values (as could be expected). A proof for this conjecture was found by F. Abi-Khuzam in 1974 (see [a2]). In [a12] and [a1] a few inequalities of similar type were proposed and subsequently proven.
References
| [a1] | F.F. Abi–Khuzam, A.B. Boghossian, "Some recent geometric inequalities" Amer. Math. Monthly , 96 (1989) pp. 576–589 |
| [a2] | F. Abi–Khuzam, "Proof of Yff's conjecture on the Brocard angle of a triangle" Elem. Math. , 29 (1974) pp. 141–142 |
| [a3] | J. Casey, "Géometrie elementaire récente" , Gauthier-Villars (1890) |
| [a4] | A.L. Crelle, "Über einige Eigenschaften des ebenen geradlinigen Dreiecks rücksichtlich dreier durch die Winkelspitzen gezogenen geraden Linien" , Berlin (1816) |
| [a5] | Ph.J. Davis, "The rise, fall, and possible transfiguration of triangle geometry: A mini-history" Amer. Math. Monthly , 102 (1995) pp. 204–214 |
| [a6] | A. Emmerich, "Die Brocardschen Gebilde und ihre Beziehungen zu den verwandten merkwürdigen Punkten und Kreisen des Dreiecks" , G. Reimer (1891) |
| [a7] | L. Guggenbuhl, "Henri Brocard and the geometry of the triangle" Math. Gazette , 80 (1996) pp. 492–500 |
| [a8] | R. Honsberger, "The Brocard angle" , Episodes in Nineteenth and Twentieth Century Euclidean Geometry , Math. Assoc. America (1995) pp. 101–106 |
| [a9] | R.A. Johnson, "Modern geometry: an elementary treatise on the geometry of the triangle and the circle" , Houghton–Mifflin (1929) (Reprinted as: Advanced Euclidean Geometry, Dover,1960) |
| [a10] | C. Kimberling, "Central points and central lines in the plane of a triangle" Math. Mag. , 67 (1994) pp. 163–187 |
| [a11] | D. Mitrinović, J.E. Pečarić, V. Volenec, "Recent advances in geometric inequalities" , Kluwer Acad. Publ. (1989) |
| [a12] | R.J. Stroeker, H.J.T. Hoogland, "Brocardian geometry revisited or some remarkable inequalities" Nieuw Arch. Wisk. 4th Ser. , 2 (1984) pp. 281–310 |
| [a13] | R.J. Stroeker, "Brocard points, circulant matrices, and Descartes' folium" Math. Mag. , 61 (1988) pp. 172–187 |
| [a14] | P. Yff, "An analogue of the Brocard points" Amer. Math. Monthly , 70 (1963) pp. 495–501 |
Brocard point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brocard_point&oldid=11736