Briot-Bouquet equation
An ordinary differential equation
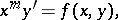 | (1) |
where 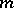 is a positive integer and the function
is a positive integer and the function 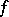 is analytic at
is analytic at 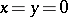 ,
, 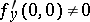 ,
, 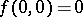 . It was shown by C. Briot and T. Bouquet [1] that any equation of the type
. It was shown by C. Briot and T. Bouquet [1] that any equation of the type
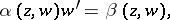 |
where 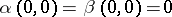 and
and 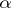 and
and 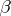 are analytic at the origin, can be reduced, by means of a special local changes of the variables, to a finite number of equations of type (1). Equation (1) always (except for the case where
are analytic at the origin, can be reduced, by means of a special local changes of the variables, to a finite number of equations of type (1). Equation (1) always (except for the case where 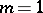 and
and 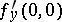 is a natural number) has a unique solution in the form of a formal power series:
is a natural number) has a unique solution in the form of a formal power series:
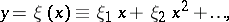 | (2) |
which converges for sufficiently small 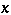 if
if 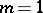 , and can diverge for all
, and can diverge for all 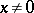 if
if 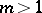 . In (1), let
. In (1), let
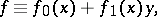 |
then, for the series (2) to converge, it is necessary and sufficient to meet 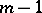 conditions concerning the coefficients of the Taylor series of
conditions concerning the coefficients of the Taylor series of 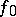 and
and 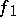 ; all the coefficients are included in these conditions, so that the existence or non-existence of an analytic solution
; all the coefficients are included in these conditions, so that the existence or non-existence of an analytic solution 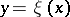 of equation (1) cannot be proved by any partial sum of the Taylor series of
of equation (1) cannot be proved by any partial sum of the Taylor series of 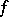 (cf. [2], [3]). For the case of a general function
(cf. [2], [3]). For the case of a general function 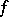 there are
there are 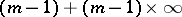 such conditions, [4]. Accordingly, the Briot–Bouquet equation is sometimes referred to as equation (1) with
such conditions, [4]. Accordingly, the Briot–Bouquet equation is sometimes referred to as equation (1) with 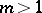 .
.
References
| [1] | C. Briot, T. Bouquet, "Récherches sur les proprietés des équations différentielles" J. École Polytechnique , 21 : 36 (1856) pp. 133–198 |
| [2] | L. Bieberbach, "Theorie der gewöhnlichen Differentialgleichungen auf funktionentheoretischer Grundlage dargestellt" , Springer (1965) |
| [3] | A.D. Bryuno, "Analytical form of differential equations. Introduction" Trans. Moscow Math. Soc. , 25 (1971) pp. 134–151 Trudy Moskov. Mat. Obshch. , 25 (1971) pp. 120–138 |
| [4] | J. Martinet, J.P. Ramis, "Problèmes de modules pour des équations différentielles du premier ordre" Publ. Math. IHES , 55 (1982) pp. 63–164 |
Briot-Bouquet equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Briot-Bouquet_equation&oldid=22189