Bregman function
Let  be a closed convex subset of
be a closed convex subset of 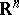 and
and 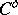 its interior. Consider a real-valued convex function (cf. also convex function (of a real variable))
its interior. Consider a real-valued convex function (cf. also convex function (of a real variable))  whose effective domain contains
whose effective domain contains  and let
and let  be defined as
be defined as
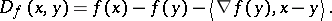 |
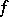 is said to be a Bregman function with zone
is said to be a Bregman function with zone 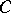 (and
(and 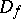 the Bregman distance induced by
the Bregman distance induced by 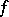 ) if the following conditions hold:
) if the following conditions hold:
B1) 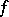 is continuously differentiable on
is continuously differentiable on 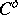 ;
;
B2) 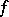 is strictly convex and continuous on
is strictly convex and continuous on  ;
;
B3) for all 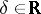 the partial level sets
the partial level sets 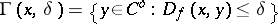 are bounded for all
are bounded for all 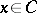 ;
;
B4) if  converges to
converges to 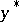 , then
, then 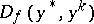 converges to
converges to  ;
;
B5) if 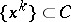 and
and  are sequences such that
are sequences such that 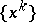 is bounded,
is bounded, 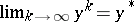 and
and 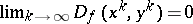 , then
, then 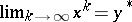 .
.
Bregman functions were introduced in [a1]. B4) and B5) hold automatically when 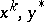 are in
are in 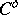 , as a consequence of B1), B2) and B3), and so they need to be checked only at points on the boundary
, as a consequence of B1), B2) and B3), and so they need to be checked only at points on the boundary 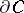 of
of 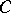 . When
. When  , a sufficient condition for a strictly convex differentiable function
, a sufficient condition for a strictly convex differentiable function 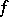 to be a Bregman function is
to be a Bregman function is
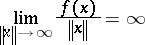 |
(see [a2]).
A Bregman function 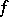 is said to be boundary coercive if for all
is said to be boundary coercive if for all 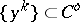 such that
such that 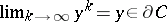 one has
one has 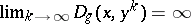 for all
for all 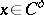 , and zone coercive if the image of
, and zone coercive if the image of  under
under 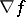 is equal to
is equal to 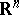 . Zone coerciveness implies boundary coerciveness (see [a3]). These notions are closely related to essential smoothness, as defined in [a5]. For a boundary-coercive Bregman function
. Zone coerciveness implies boundary coerciveness (see [a3]). These notions are closely related to essential smoothness, as defined in [a5]. For a boundary-coercive Bregman function 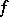 the zone
the zone 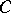 is uniquely determined from
is uniquely determined from 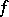 , i.e.
, i.e. 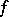 cannot be finitely extended outside
cannot be finitely extended outside 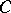 . This property is essential in most applications of Bregman functions.
. This property is essential in most applications of Bregman functions.
Examples.
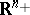 denotes the non-negative orthant of
denotes the non-negative orthant of 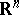 .
.
i) 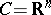 ,
, 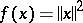 . In this case
. In this case 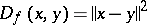 . More generally,
. More generally, 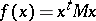 , with
, with  symmetric and positive definite, in which case
symmetric and positive definite, in which case 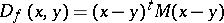 .
.
ii) 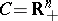 ,
, 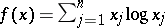 , extended by continuity to
, extended by continuity to 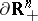 with the convention that
with the convention that 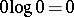 . In this case
. In this case
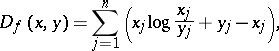 |
which is the Kullback–Leibler information divergence, widely used in statistics (see Kullback–Leibler-type distance measures; [a4]).
iii) 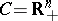 ,
, 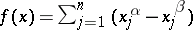 with
with 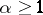 ,
, 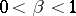 . For
. For 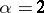 ,
, 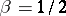 one has
one has
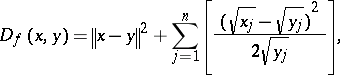 |
and for 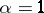 ,
,  one has
one has
 |
iv) 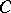 is a box (i.e.,
is a box (i.e., 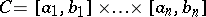 with
with 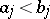 ,
, 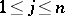 ),
),
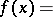 |
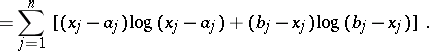 |
In this case
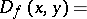 |
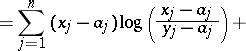 |
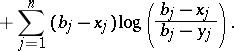 |
v)  is a polyhedron with non-empty interior (i.e.,
is a polyhedron with non-empty interior (i.e.,  with
with 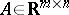 ,
, 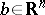 and
and 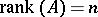 (so that
(so that 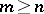 )),
)), 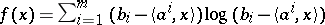 , where
, where  (
(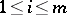 ) are the rows of
) are the rows of 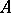 . In this case
. In this case
 |
 |
All the Bregman functions in the above examples are zone coercive, except for iii) with 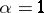 , which is only boundary coercive.
, which is only boundary coercive.
Bregman functions are used in algorithms for convex feasibility problems and linearly constrained convex optimization (cf. Bregman distance), as well as for generalizations of the proximal point method for convex optimization (cf. Proximal point methods in mathematical programming).
References
| [a1] | L.M. Bregman, "The relaxation method of finding the common points of convex sets and its application to the solution of problems in convex programming" USSR Comput. Math. Math. Phys. , 7 : 3 (1967) pp. 200–217 (In Russian) |
| [a2] | A.R. de Pierro, A.N. Iusem, "A relaxed version of Bregman's method for convex programming" J. Optimization Th. Appl. , 51 (1986) pp. 421–440 |
| [a3] | A.N. Iusem, "On some properties of generalized proximal point methods for quadratic and linear programming" J. Optimization Th. Appl. , 85 (1995) pp. 593–612 |
| [a4] | F. Liese, I. Vajda, "Convex statistical distances" , Teubner (1987) |
| [a5] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) |
Bregman function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bregman_function&oldid=16823