Brauer second main theorem
For notation and definitions, see Brauer first main theorem.
Let  be an element of
be an element of  whose order is a power of
whose order is a power of 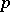 . The
. The 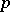 -section of
-section of 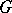 associated to
associated to  is the set of all elements of
is the set of all elements of 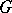 whose
whose 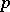 -part is conjugate to
-part is conjugate to  . Brauer second main theorem relates the values of irreducible characters of
. Brauer second main theorem relates the values of irreducible characters of 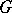 on the
on the 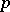 -section associated to
-section associated to  to values of characters in certain blocks of
to values of characters in certain blocks of 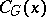 .
.
Suppose that 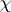 is an irreducible character of
is an irreducible character of 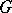 (cf. also Character of a group), afforded by the
(cf. also Character of a group), afforded by the 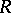 -free right
-free right 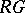 -module
-module 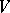 , and belonging to the block
, and belonging to the block 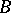 (cf. also Defect group of a block). Let
(cf. also Defect group of a block). Let  be a
be a 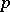 -element of
-element of 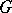 , and let
, and let 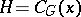 . For all
. For all 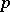 -subgroups
-subgroups 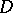 of
of 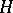 ,
, 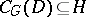 ; hence
; hence 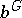 is defined for all blocks
is defined for all blocks 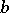 of
of 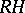 . One can organize the block decomposition of
. One can organize the block decomposition of 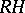 as
as 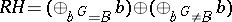 . Let
. Let  be the projection of
be the projection of 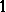 on
on 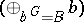 , and let
, and let 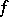 be the projection of
be the projection of 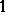 on
on 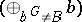 . The restriction
. The restriction 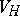 of
of 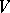 to
to 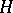 can be decomposed as
can be decomposed as 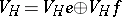 . If
. If 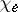 is the character of
is the character of 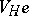 and
and 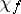 is the character of
is the character of 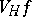 , then of course
, then of course 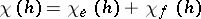 for all
for all 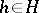 . Brauer's second main theorem states that for all elements
. Brauer's second main theorem states that for all elements 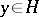 of order prime to
of order prime to 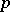 ,
, 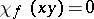 . Thus, the values of
. Thus, the values of 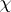 on the
on the 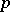 -section associated to
-section associated to  are determined in the blocks of
are determined in the blocks of 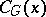 sent to
sent to 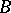 by the Brauer correspondence (cf. also Brauer first main theorem).
by the Brauer correspondence (cf. also Brauer first main theorem).
This theorem was first proved in [a1]. See also [a2], [a3], and [a4].
References
| [a1] | R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" Math. Z. , 72 (1959) pp. 22–46 |
| [a2] | C. Curtis, I. Reiner, "Methods of representation theory" , II , Wiley (1987) |
| [a3] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) |
| [a4] | H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987) |
Brauer second main theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brauer_second_main_theorem&oldid=18936