Branching processes, regularity of
A property of branching processes ensuring that the number of particles at any moment of time is finite. The problem of the regularity of a branching process is usually reduced to the problem of uniqueness of the solution of some differential or integral equation. For instance, in a continuous-time branching process the differential equation
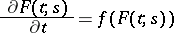 |
with the initial condition 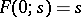 has a unique solution if and only if, for any
has a unique solution if and only if, for any 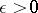 , the integral
, the integral
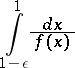 |
is divergent. In the branching Bellman–Harris process the generating function 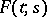 of the number of particles is the solution of the non-linear integral equation
of the number of particles is the solution of the non-linear integral equation
 | (*) |
where 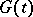 is the distribution function of the lifetimes of particles and
is the distribution function of the lifetimes of particles and 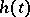 is the generating function of the number of daughter particles ( "direct descendants" ) of a single particle. If, for given
is the generating function of the number of daughter particles ( "direct descendants" ) of a single particle. If, for given 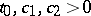 and an integer
and an integer 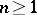 , the inequalities
, the inequalities
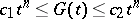 |
are valid for all 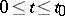 , the solution of equation (*) is unique if and only if the equation
, the solution of equation (*) is unique if and only if the equation
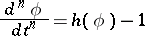 |
with initial conditions
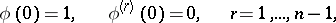 |
has a unique solution
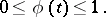 |
For a branching process described by equation (*) to be regular, it is necessary and sufficient for the integral
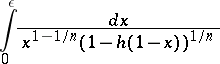 |
to diverge for any 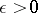 .
.
References
| [1] | B.A. [B.A. Sevast'yanov] Sewastjanow, "Verzweigungsprozesse" , Akad. Wissenschaft. DDR (1974) (Translated from Russian) |
Comments
Additional references can be found in the article Branching process.
Branching processes, regularity of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branching_processes,_regularity_of&oldid=11240