Branching process with diffusion
A model of a branching process in which the reproducing particles diffuse in some domain 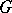 . Let the domain
. Let the domain 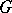 be
be  -dimensional, with an absorbing boundary
-dimensional, with an absorbing boundary 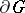 , and let the particles in the domain itself execute mutually independent Brownian motions. Each particle in
, and let the particles in the domain itself execute mutually independent Brownian motions. Each particle in 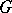 is independently converted, within a time
is independently converted, within a time 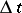 , into
, into  particles with a probability of
particles with a probability of 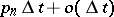 ,
, 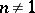 ,
,  . Let the daughter particles begin their independent evolution from the point of their genesis. Let
. Let the daughter particles begin their independent evolution from the point of their genesis. Let
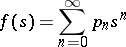 |
be the generating function of 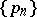 , let
, let 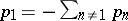 , and let
, and let 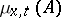 be the number of particles in a set
be the number of particles in a set 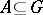 at the moment
at the moment 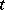 if there initially was one particle at the point
if there initially was one particle at the point 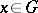 . The generating functional
. The generating functional
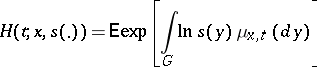 |
satisfies the quasi-linear parabolic equation
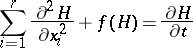 |
with the initial condition
 |
and the boundary condition
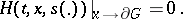 |
Denote by 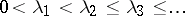 the eigen values, and let
the eigen values, and let 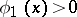 be the eigen function of the problem
be the eigen function of the problem
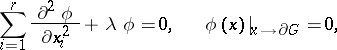 |
corresponding to 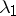 . As
. As 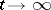 the asymptotic relation
the asymptotic relation
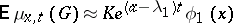 |
holds. For this reason the problem is said to be subcritical if 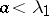 , critical if
, critical if 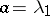 and supercritical if
and supercritical if 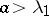 . If
. If 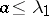 , a branching process with diffusion dies out with probability one, while if
, a branching process with diffusion dies out with probability one, while if 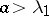 , both the probability of dying out and the probability of the event
, both the probability of dying out and the probability of the event 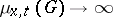 as
as 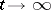 will in general be positive. Depending on their criticality, branching processes with diffusion obey limit theorems analogous to those valid for branching processes without diffusion.
will in general be positive. Depending on their criticality, branching processes with diffusion obey limit theorems analogous to those valid for branching processes without diffusion.
References
| [1] | B.A. [B.A. Sevast'yanov] Sewastjanow, "Verzweigungsprozesse" , Akad. Wissenschaft. DDR (1974) (Translated from Russian) |
Comments
Additional references can be found in the article Branching process.
Branching process with diffusion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branching_process_with_diffusion&oldid=46154