Branching process with a random medium

branching process in a random medium

A time-inhomogeneous branching process in which the inhomogeneity is random. Let 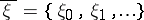be a stationary sequence of random variables (the value of 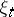is interpreted as the state of the "medium" at the moment of time 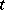), and let to each possible state of the medium 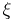correspond a probability distribution 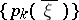of the number of descendants of a single particle:

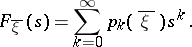In order to construct a trajectory 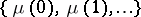of a branching process in a random medium the value of 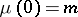and the trajectory 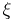of the states of the medium are fixed, and 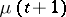is determined for each 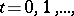as a sum of 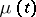independent random variables with distribution 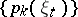. Such a complication of the branching Galton–Watson process is natural if, for example, the branching process in a random medium is regarded as a model of a biological population.

The properties of branching processes in a random medium are analogous to those of ordinary branching processes. For instance, the generating distribution function of 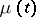, under the condition 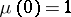, has the form

(*)

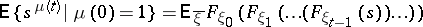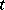(for a branching Galton–Watson process, i.e. for , the right-hand side of (*) equals the -fold iteration of 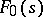). Branching processes in a random medium may be subcritical, critical and supercritical: the "criticality parameter" here (see [1]) is the variable

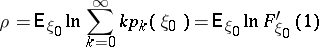(for ordinary branching processes, the "criticality parameter" is the mathematical expectation of the number of "descendants" of a single particle). If , the branching process in a random medium is said to be subcritical and, for the random variable

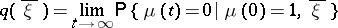which is the probability of extinction of the branching process in a random medium for a given trajectory 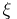, the relation

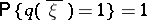is valid. There is also the analogue of the limit theorem of the subcritical Galton–Watson branching process: For almost all realizations of the sequence 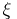the limits

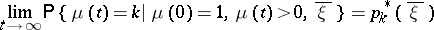exist and satisfy

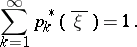If 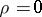, the branching process in a random medium is said to be critical, and

and, for almost all realizations of ,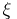

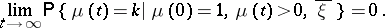If 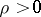, the branching process in a random medium is said to be supercritical; in such a case

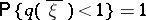and, if certain additional conditions are met, there exists for almost all 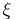a non-negative random variable ,

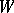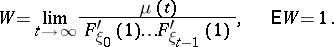References

[1]	K.B. Athreya, P.E. Ney, "Branching processes" , Springer (1972)

Comments

Additional references can be found in the article Branching process.