Branching process with a finite number of particle types

A model of a branching process which is a special case of a Markov process with a countable set of states. The state of the branching vector is described by the random process

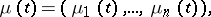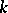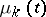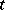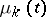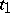the -th component, , of which shows that at time there are particles of type . The principal property by which branching processes differ from Markov processes is that the particles existing at the moment produce daughter particles at any subsequent moment 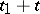, , 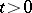in a mutually independent manner. The generating functions

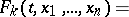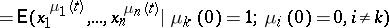satisfy the system of equations

(*)

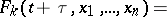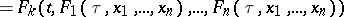with initial conditions

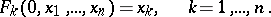The equations (*) are satisfied by discrete-time and continuous-time processes.

In the case of discrete time, the matrix of mathematical expectations

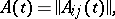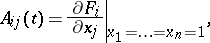is the 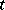-th power of the matrix 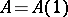: 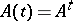. If 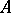is indecomposable and aperiodic, it has a simple positive eigen value 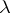which is larger than the moduli of the other eigen values. In this case, as ,

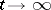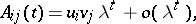where 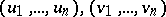are the right and left eigen vectors of 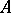which correspond to 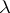. Branching processes with an indecomposable matrix 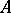are said to be subcritical if 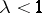, supercritical if 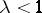and critical if 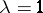and if at least one of the functions is non-linear. The concept of criticality is defined in a similar manner for continuous-time processes.

The asymptotic properties of a branching process significantly depend on its criticality. Subcritical and critical processes die out with probability one. The asymptotic formulas (as 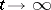) for the probabilities,

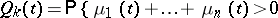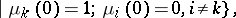and the theorems on limit distributions of the number of particles [2], are analogous to the respective results for processes involving single-type particles (cf. Branching process). Asymptotic properties in the near-critical case (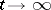, ) have been studied [3]. Processes with a decomposable matrix of mathematical expectations have also been investigated [4].

References

[1]	A.N. Kolmogorov, N.A. Dmitriev, "Branching stochastic processes" Dokl. Akad. Nauk SSSR , 56 : 1 (1947) pp. 5–8 (In Russian)
[2]	B.A. [B.A. Sevast'yanov] Sewastjanow, "Verzweigungsprozesse" , Akad. Wissenschaft. DDR (1974) (Translated from Russian)
[3]	V.P. Chistyakov, "On transition phenomena in branching stochastic processes with several types of particles" Theory Probab. Appl. , 17 : 4 (1972) pp. 631–639 Teor. Veroyatnost. i Primenen. , 17 : 4 (1972) pp. 669–678
[4]	Y. Ogura, "Asymptotic behaviour of multitype Galton–Watson processes" J. Math. Kyoto Univ. , 15 (1975) pp. 251–302

Comments

Additional references can be found in the article Branching process.