Branching point (of a minimal surface)

A singular point of a minimal surface in which the first fundamental form of the surface vanishes; this means, in fact, that such a branching point can exist on a generalized minimal surface only. This singular point owes its name to the fact that in a neighbourhood of it the structure of the generalized minimal surface resembles that of the Riemann surface of the function , , over the point , i.e. there the generalized minimal surface has a many-sheeted orthogonal projection onto some plane domain, in which the projection of the branching point itself is an interior point with a unique pre-image. In a neighbourhood of a branching point the coordinates of the minimal surface can be represented in the form

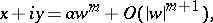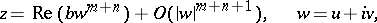where and are two complex constants, 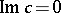; 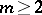, and are integers named, respectively, the order and the index of the singular point and and are intrinsic isothermal coordinates.

The following theorem was deduced on the basis of this representation: If the numbers and 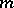are coprime, then the minimal surface has 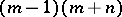different lines of self-intersection issuing from the singular point in different directions. There is a relation between the genus of a complete minimal surface, the number of its branching points, and the index of its Gaussian mapping [1].

One distinguishes between two kinds of branching points: false branching points and true (non-false) branching points. False branching points are singularities of the mapping which defines the surface that can be got rid of by re-parametrization (e.g. if 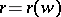is a regular minimal surface, then the generalized minimal surface has a false branching point at ). A true branching point represents a real singularity of the surface itself, and has the following important property: In a neighbourhood of a true branching point the surface can be altered so that the new surface which coincides with the original one outside the deformed neighbourhood will have a smaller area than the original surface (this holds for surfaces in 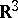but is not true in more-general settings: e.g. for the area-minimizing surfaces in 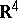). The theory of generalized minimal surfaces with a branching point served as a base of the general theory of branched immersions, developed for a broad class of two-dimensional surfaces in 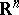, , 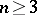[2].

References

[1]	Y.W. Chen, "Branch points, poles and planar points of minimal surfaces in 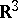" Ann. of Math. , 49 : 4 (1948) pp. 790–806
[2]	J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1973)