Branch of an analytic function
The result of analytic continuation of a given element of an analytic function represented by a power series
 |
with centre  and radius of convergence
and radius of convergence 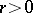 along all possible paths belonging to a given domain
along all possible paths belonging to a given domain  of the complex plane
of the complex plane 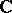 ,
, 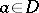 . Thus, a branch of an analytic function is defined by the element
. Thus, a branch of an analytic function is defined by the element  and by the domain
and by the domain  . In calculations one usually employs only single-valued, or regular, branches of analytic functions, which exist not for all domains
. In calculations one usually employs only single-valued, or regular, branches of analytic functions, which exist not for all domains 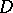 belonging to the domain of existence of the complete analytic function. For instance, in the cut complex plane
belonging to the domain of existence of the complete analytic function. For instance, in the cut complex plane 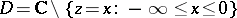 the multi-valued analytic function
the multi-valued analytic function 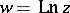 has the regular branch
has the regular branch
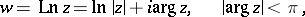 |
which is the principal value of the logarithm, whereas in the annulus 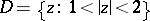 it is impossible to isolate a regular branch of the analytic function
it is impossible to isolate a regular branch of the analytic function  .
.
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 Chapt. 3; 2, Chapt. 4 , Springer (1964) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
Branch of an analytic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branch_of_an_analytic_function&oldid=16288