Branch group
The class of branch groups is recently (1999) defined, and consists of groups with many remarkable properties. It is one of three classes that naturally partition the class of just infinite groups (i.e. infinite groups with finite proper quotients). There are two (non-equivalent) ways to define the class of branch groups.
The first definition is as follows: A branch group is a group $G$ which has a descending sequence $\{ H _ { n } \} _ { n = 1 } ^ { \infty }$ of normal subgroups (cf. also Normal subgroup) such that for any $n \geq 1$:
i) $[G : H ] < \infty$;
ii) $H _ { n } \cong L _ { n } \times \ldots \times L _ { n }$ (with $M _ { n }$ factors) for some group $L_{n}$ and integer $M _ { n }$;
iii) the factorization for $H _ { n + 1}$ subdivides the factorization for $H _ { n }$; in particular, $M _ { n+ 1} / M _ { n }$ is an integer $\geq 2$;
iv) the group $G$ acts transitively by conjugation on the set of factors of $H _ { n }$ (cf. also Transitive group).
Another version of the definition uses an action of $G$ on rooted trees. Let $\overline { m } = \{ m _ { n } \} _ { n = 0 } ^ { \infty }$ be a sequence of integers $\geq 2$, called a branch index. Let $T _ { \overline{m} }$ be a spherically homogeneous rooted tree (cf. also Tree) determined by $m$. It has a root vertex $\emptyset$, it has $M _ { n } = m _ { 0 } \ldots m _ { n - 1}$ vertices on level $n$, and 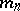 is a branch index for level $n$ (i.e. every vertex $u$ of the level $| u | = n$ has
is a branch index for level $n$ (i.e. every vertex $u$ of the level $| u | = n$ has 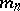 successors). Let $V$ be a set of vertices of the tree $T$.
successors). Let $V$ be a set of vertices of the tree $T$.
For a group $G$ acting by automorphisms on $T$ (cf. also Automorphism) one defines following subgroups:
$\operatorname { St } _ { G } ( u ) = \{ g \in G : u ^ { g } = u \}$, a stabilizer of the vertex $u \in V$ (cf. also Stabilizer);
$\operatorname { St } _ { G } ( n ) = \cap _ { | u | = n } \operatorname { St } _ { G } ( u )$, a stabilizer of level $n$;
$\operatorname {rist}_{G} ( u ) = \{ g \in G : g \ \text {acts trivially on } T \backslash T _ { u } \}$, a rigid stabilizer of vertex $u$ ($T _ { u }$ is a subtree of $T$ with a root vertex $u$);
$\operatorname { rist } _ { G } ( n ) = \langle \operatorname { rist } _ { G } ( u ) : | u | = n \rangle$, a rigid stabilizer of level $n$ (i.e. the group generated by the rigid stabilizers of the vertices of level $n$). It is clear that $\operatorname { rist } _ { G } ( n )$ decomposes as a direct product of groups $\operatorname {rist}_{G} ( u )$, $| u | = n$. The subgroups $\operatorname { St } _ { G } ( u )$ and $\operatorname { St } _ { G } ( n )$ have finite index in $G$, while $\operatorname {rist}_{G} ( u )$ and $\operatorname { rist } _ { G } ( n )$ can be trivial subgroups.
An action of $G$ on $T$ is called spherically transitive if it is transitive on each level $n = 1,2 , \dots$; in this case stabilizers and rigid stabilizers of vertices of the same level are conjugate in $G$.
Now, a group $G$ is called a branch group if there is a faithful spherically transitive action of $G$ on some tree $T _ { \overline{m} }$ such that $[G:\operatorname{rist}_G ( n )]<\infty$ for any $n \geq 1$.
A group satisfying the last definition also satisfies the first, with $H _ { n } = \operatorname { rist } _ { G } ( n )$ and $L_{n}$ being an isomorphic type of groups $\operatorname {rist}_{G} ( u )$, $| u | = n$. The opposite is not correct. For the class of just infinite groups both definitions are equivalent.
A profinite branch group is defined in the same manner as above, only all groups involved have to be closed subgroups in $G$ or in $\operatorname{Aut}T$, considered as a profinite group.
The importance of the class of branch groups follows from the following theorem [a3], [a9]: Let $G$ be an abstract just infinite group. Then either $G$ is a branch group or $G$ contains a normal subgroup of finite index which is isomorphic to a direct product of a finite number of copies of a group $L$, where $L$ is either a simple group or a hereditarily just infinite group (i.e. a residually-finite group with just infinite subgroups of finite index).
For profinite just infinite groups, this trichotomy becomes a dichotomy, as simple groups cannot occur.
The class of just infinite branch groups coincides with the class of just infinite groups with an infinite structural lattice of normal subgroups [a10]. The first finitely-generated just infinite branch groups were constructed in [a4], [a5], [a6], [a8], [a7].
Since every finitely-generated infinite group can be mapped onto a just infinite group, the above theorem shows that the class of branch groups should contain groups with many specific properties that are stable under the factorization. This has been confirmed by many investigations. Namely in [a4], [a5], [a6], [a8], [a7] it was shown that for any prime number $p$ there is a finitely-generated branch torsion $p$-group (cf. also $p$-group).
In [a5], [a6], [a7] the first examples of groups of intermediate growth between polynomial and exponential are constructed (cf. also Polynomial and exponential growth in groups and algebras).
Examples of branch groups of finite width (i.e with uniformly bounded ranks of quotients of lower central series) are considered in [a1].
Applications of branch groups to the theory of the discrete Laplace operator on graphs are given in [a2].
For more information on branch groups, see [a3].
References
| [a1] | L. Bartholdi, R.I. Grigorchuk, "Lie methods in growth of groups and groups of finite width" , Proc. Conf. Group Theory Edinburg 1998 (to appear) |
| [a2] | L. Bartholdi, R.I. Grigorchuk, "On the spectrum of Hecke type operators related to some fractal groups" (to appear) |
| [a3] | R.I. Grigorchuk, "Just infinite branch groups" M. du Santoy (ed.) D. Segal (ed.) , Horizons in Profinite Groups , Birkhäuser (to appear) |
| [a4] | R.I. Grigorchuk, "On the Burnside problem for periodic groups" Funct. Anal. Appl. , 14 (1980) pp. 41–43 |
| [a5] | R.I. Grigorchuk, "On Milnor's problem on group growth" Soviet Math. Dokl. , 28 (1983) pp. 23–26 |
| [a6] | R.I. Grigorchuk, "The growth degrees of finitely generated groups and the theory of invariant means" Izv. Akad. Nauk. SSSR Ser. Mat. , 48 : 5 (1984) pp. 939–985 |
| [a7] | R.I. Grigorchuk, "Degrees of growth of $p$-groups and torsion free groups" Mat. Sb. (N.S.) , 126 : 168:2 (1985) pp. 194–214 |
| [a8] | N. Gupta, S Sidki, "On the Burnside problem for periodic groups" Math. Z. , 182 (1983) pp. 385–388 |
| [a9] | J.S. Wilson, "Abstract and profinite just infinite groups" M. du Santoy (ed.) D. Segal (ed.) , Horizons in Profinite Groups , Birkhäuser (to appear) |
| [a10] | J.S. Wilson, "Groups with every proper quotient finite" Proc. Cambridge Philos. Soc. , 69 (1971) pp. 373–391 |
Branch group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branch_group&oldid=55420