Braess paradox
The words "Braess's paradox" refer to a surprising decrease in performance for some network, which is a result of it being improved locally. The occurrence of this decrease has been studied in mathematical models of equilibrium flow in road/rail traffic, computer networks, telephone networks, water supply systems, electrical circuits, spring systems, and so on. This has been done under various assumptions on routing schemes, such as being state-dependent or fixed.
Below, the occurrence of Braess's paradox in a classical model of user equilibrium traffic flow is given.
Let  be a finite directed graph, with node set
be a finite directed graph, with node set  and arc, branch or link set
and arc, branch or link set  (cf. also Graph, oriented). A path in which all links are similarly directed is called a route, with the initial and final nodes forming an origin/destination pair (or O/D pair). One considers a set
(cf. also Graph, oriented). A path in which all links are similarly directed is called a route, with the initial and final nodes forming an origin/destination pair (or O/D pair). One considers a set  of O/D pairs, and for each
of O/D pairs, and for each  , supposes a flow demand
, supposes a flow demand 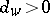 to be given. Let
to be given. Let  be a set of routes joining
be a set of routes joining  . For each
. For each 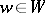 , and
, and 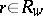 , one considers
, one considers 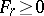 such that
such that 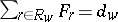 , giving a route flow vector
, giving a route flow vector 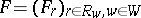 . This route flow induces a link flow
. This route flow induces a link flow  , by
, by 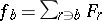 for each
for each 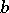 , where one identifies a route with the set of its links. For each link
, where one identifies a route with the set of its links. For each link  , one supposes a link cost
, one supposes a link cost 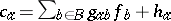 , where
, where 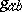 and
and 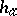 are given. For
are given. For 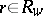 ,
, 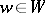 , one defines a route cost by
, one defines a route cost by 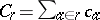 .
.
A route flow 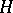 is a user equilibrium if it satisfies the condition that for all
is a user equilibrium if it satisfies the condition that for all 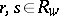 ,
,  , if
, if 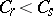 then
then 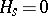 . In other words, there is, for each
. In other words, there is, for each 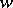 , a common route cost
, a common route cost 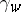 for all routes
for all routes 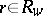 with non-zero
with non-zero 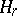 . A user equilibrium flow exists always [a5], and if the matrix
. A user equilibrium flow exists always [a5], and if the matrix  is such that
is such that 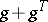 is positive-definite, then the equilibrium link flows, and hence the route costs
is positive-definite, then the equilibrium link flows, and hence the route costs 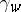 , are unique. In [a3], Braess's paradox is said to occur if adding a new route
, are unique. In [a3], Braess's paradox is said to occur if adding a new route  to some
to some 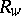 results in
results in 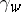 being increased. See also [a3] for necessary and sufficient conditions for this to happen under the assumption that there is a strictly positive equilibrium flow in all routes.
being increased. See also [a3] for necessary and sufficient conditions for this to happen under the assumption that there is a strictly positive equilibrium flow in all routes.
There is no fixed definition of Braess's paradox in all systems, but there is a common theme. One assumes some measure of performance,  , such as
, such as 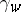 . On the network given by any one link
. On the network given by any one link 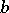 ,
, 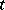 depends on the flow
depends on the flow  and a parameter
and a parameter  . For example,
. For example, 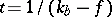 if the link is given by an M/M/1 queue (cf. also Queue). Note that
if the link is given by an M/M/1 queue (cf. also Queue). Note that 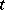 decreases if
decreases if  increases, for
increases, for  fixed. Suppose some flow demand is fixed and link flows are given by some requirement about equilibria, or by a given dynamical process not in equilibrium. One says that Braess's paradox occurs if, for the network as a whole,
fixed. Suppose some flow demand is fixed and link flows are given by some requirement about equilibria, or by a given dynamical process not in equilibrium. One says that Braess's paradox occurs if, for the network as a whole, 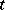 increases when some
increases when some 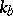 increases. Adding links may be thought of as changing a parameter
increases. Adding links may be thought of as changing a parameter 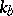 from zero or infinity. A different language would be used to describe certain other types of networks, such as electrical circuits.
from zero or infinity. A different language would be used to describe certain other types of networks, such as electrical circuits.
Under this description, the Downs–Thomson paradox [a4] is a particular type of Braess's paradox. If one distinguishes these paradoxes mathematically, it is by requiring the link costs 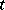 in the Braess paradox to be increasing functions of the link flow
in the Braess paradox to be increasing functions of the link flow 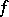 , while in the Downs–Thomson paradox there is a link with
, while in the Downs–Thomson paradox there is a link with 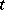 a decreasing function of
a decreasing function of 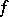 .
.
Independent discoveries of Braess's paradox can be attributed to D. Braess [a1], A. Downs [a4], J.M. Thomson [a6] and C.A. Zukowski and J.L. Wyatt [a7].
[a2] contains an ample list of references.
References
| [a1] | D. Braess, "Über ein Paradoxon aus der Verkehrsplannung" Unternehmensforschung , 12 (1968) pp. 258–268 |
| [a2] | D. Braess, http://homepage.ruhr-uni-bochum.de/Dietrich.Braess (2000) |
| [a3] | S. Dafermos, A. Nagurney, "On some traffic theory equilibrium paradoxes" Transportation Res. B , 18 (1984) pp. 101–110 |
| [a4] | A. Downs, "The law of peak-hour expressway congestion" Traffic Quart. , 16 (1962) pp. 393–409 |
| [a5] | M.J. Smith, "The existence, uniqueness, and stability of traffic equilibria" Transportation Res. B , 13 (1979) pp. 295–304 |
| [a6] | J.M. Thomson, "Great cities and their traffic" , Gollancz, London (1977) |
| [a7] | C.A. Zukowski, J.L. Wyatt, "Sensitivity of nonlinear one-port resistor networks" IEEE Trans. Circuits Syst. , CAS-31 (1984) pp. 1048–1051 |
Braess paradox. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Braess_paradox&oldid=16356