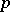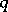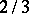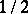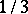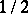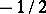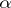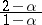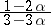Box-Cox transformation
Transformations of data designated to achieve a specified purpose, e.g., stability of variance, additivity of effects and symmetry of the density. If one is successful in finding a suitable transformation, the ordinary method for analysis will be available. Among the many parametric transformations, the family in [a1] is commonly utilized.
Let  be a random variable on the positive half-line. Then the Box–Cox transformation of
be a random variable on the positive half-line. Then the Box–Cox transformation of  with power parameter
with power parameter  is defined by:
is defined by:
 |
The formula  is chosen so that
is chosen so that  is continuous as
is continuous as 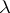 tends to zero and monotone increasing with respect to
tends to zero and monotone increasing with respect to  for any
for any 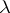 .
.
The power parameter 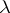 is estimated by a graphical technique or by the maximum-likelihood method. Unfortunately, a closed form for the estimator
is estimated by a graphical technique or by the maximum-likelihood method. Unfortunately, a closed form for the estimator 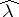 can be rarely found. Hence, the plot of the maximum likelihood against
can be rarely found. Hence, the plot of the maximum likelihood against 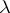 is helpful. The value of
is helpful. The value of 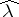 obtained in this way is treated as if it were a true value, and then one fits the model to the transformed data. Such an approach may be easily carried out, and an asymptotic theory associated with other parameters is useful. See [a1] and [a3].
obtained in this way is treated as if it were a true value, and then one fits the model to the transformed data. Such an approach may be easily carried out, and an asymptotic theory associated with other parameters is useful. See [a1] and [a3].
This treatment has, however, some difficulties because  has a variability and depends on the given data itself. It is known that estimation of
has a variability and depends on the given data itself. It is known that estimation of 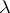 by maximum likelihood and related likelihood-ratio tests can be heavily influenced by outliers (cf. also Outlier). Further, in certain situations, the usual limiting theory based on knowing
by maximum likelihood and related likelihood-ratio tests can be heavily influenced by outliers (cf. also Outlier). Further, in certain situations, the usual limiting theory based on knowing 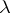 does not hold in the unknown case. Therefore, several robust estimation procedures have been proposed (see Robust statistics; and [a5] and references therein).
does not hold in the unknown case. Therefore, several robust estimation procedures have been proposed (see Robust statistics; and [a5] and references therein).
In the literature, Box–Cox transformations are applied to basic distributions, e.g., the cubic root transformation of chi-squared variates is used for acceleration to normality (cf. also Normal distribution), and the square-root transformation stabilizes variances of Poisson distributions (cf. also Poisson distribution). These results are unified by appealing to features of the following family of distributions.
Consider a collection of densities of the form
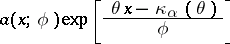 |
satisfying 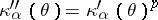 with
with 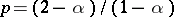 . This family is called an exponential dispersion model with power variance function (EDM-PVF) of index
. This family is called an exponential dispersion model with power variance function (EDM-PVF) of index 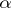 . The existence of such a model was shown in [a2] unless
. The existence of such a model was shown in [a2] unless 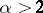 or
or 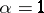 . It is a flexible family, including the normal, Poisson, gamma-, inverse Gaussian, etc., distributions.
. It is a flexible family, including the normal, Poisson, gamma-, inverse Gaussian, etc., distributions.
It is known that both of the normalizing and the variance-stabilizing transformations of the exponential dispersion model with power variance function are given by Box–Cox transformations, see [a4]. If 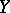 follows the exponential dispersion model with power variance function and with index
follows the exponential dispersion model with power variance function and with index 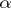 , the normalizing and variance-stabilizing transformations are given by
, the normalizing and variance-stabilizing transformations are given by 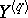 , respectively
, respectively 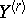 , where
, where 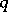 (the power for normalization) and
(the power for normalization) and  (the power for variance-stabilization) are summarized in the Table below (recall that
(the power for variance-stabilization) are summarized in the Table below (recall that 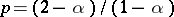 ). The similar characteristics of familiar distributions are also tabulated there. For
). The similar characteristics of familiar distributions are also tabulated there. For 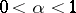 , it has been proved in [a4] that the density of
, it has been proved in [a4] that the density of 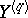 has a uniformly convergent Gram–Charlier expansion (cf. also Gram–Charlier series). This implies that the normalizing transformation which is obtained by reducing the third-order cumulant reduces all higher-order cumulants as a result (cf. also Cumulant).'
has a uniformly convergent Gram–Charlier expansion (cf. also Gram–Charlier series). This implies that the normalizing transformation which is obtained by reducing the third-order cumulant reduces all higher-order cumulants as a result (cf. also Cumulant).'
<tbody> </tbody>
|
Box–Cox transformations are also applied to link functions in generalized linear models. The transformations mainly aim to get the linearity of effects of covariates. See [a3] for further detail. Generalized Box–Cox transformations for random variables and link functions can be found in [a5].
See also Exponential distribution; Regression.
References
| [a1] | G.E.P. Box, D.R. Cox, "An analysis of transformations" J. Roy. Statist. Soc. B , 26 (1964) pp. 211–252 |
| [a2] | B. Jørgensen, "Exponential dispersion models" J. Roy. Statist. Soc. B , 49 (1987) pp. 127–162 |
| [a3] | P. McCullagh, J.A. Nelder, "Generalized linear models" , Chapman and Hall (1990) (Edition: Second) |
| [a4] | R. Nishii, "Convergence of the Gram–Charlier expansion after the normalizing Box–Cox transformation" Ann. Inst. Statist. Math. , 45 : 1 (1993) pp. 173–186 |
| [a5] | G.A.F. Seber, C.J. Wild, "Nonlinear regression" , Wiley (1989) |
Box-Cox transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Box-Cox_transformation&oldid=11455