Bounded operator
A mapping  of a topological vector space
of a topological vector space  into a topological vector space
into a topological vector space  such that
such that  is a bounded subset in
is a bounded subset in  for any bounded subset
for any bounded subset  of
of  . Every operator
. Every operator  , continuous on
, continuous on  , is a bounded operator. If
, is a bounded operator. If 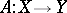 is a linear operator, then for
is a linear operator, then for 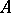 to be bounded it is sufficient that there exists a neighbourhood
to be bounded it is sufficient that there exists a neighbourhood 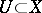 such that
such that 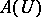 is bounded in
is bounded in 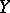 . Suppose that
. Suppose that 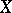 and
and 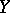 are normed linear spaces and that the linear operator
are normed linear spaces and that the linear operator 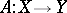 is bounded. Then
is bounded. Then
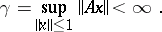 |
This number is called the norm of the operator 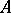 and is denoted by
and is denoted by 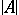 . Then
. Then
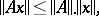 |
and 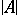 is the smallest constant
is the smallest constant 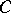 such that
such that
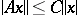 |
for any 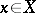 . Conversely, if this inequality is satisfied, then
. Conversely, if this inequality is satisfied, then 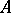 is bounded. For linear operators mapping a normed space
is bounded. For linear operators mapping a normed space 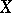 into a normed space
into a normed space 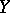 , the concepts of boundedness and continuity are equivalent. This is not the case for arbitrary topological vector spaces
, the concepts of boundedness and continuity are equivalent. This is not the case for arbitrary topological vector spaces 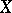 and
and 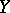 , but if
, but if 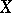 is bornological and
is bornological and 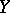 is a locally convex space, then the boundedness of a linear operator
is a locally convex space, then the boundedness of a linear operator 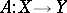 implies its continuity. If
implies its continuity. If 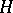 is a Hilbert space and
is a Hilbert space and 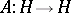 is a bounded symmetric operator, then the quadratic form
is a bounded symmetric operator, then the quadratic form 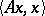 is bounded on the unit ball
is bounded on the unit ball 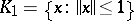 . The numbers
. The numbers
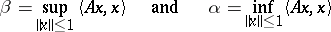 |
are called the upper and lower bounds of the operator 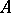 . The points
. The points  and
and 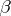 belongs to the spectrum of
belongs to the spectrum of 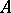 , and the whole spectrum lies in the interval
, and the whole spectrum lies in the interval 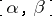 . Examples of bounded operators are: the projection operator (projector) onto a complemented subspace of a Banach space, and an isometric operator acting on a Hilbert space.
. Examples of bounded operators are: the projection operator (projector) onto a complemented subspace of a Banach space, and an isometric operator acting on a Hilbert space.
If the space 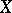 and
and 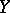 have the structure of a partially ordered set, for example are vector lattices (cf. Vector lattice), then a concept of order-boundedness of an operator can be introduced, besides the topological boundedness considered above. An operator
have the structure of a partially ordered set, for example are vector lattices (cf. Vector lattice), then a concept of order-boundedness of an operator can be introduced, besides the topological boundedness considered above. An operator 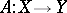 is called order-bounded if
is called order-bounded if 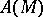 is an order-bounded set in
is an order-bounded set in 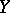 for any order-bounded set
for any order-bounded set 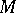 in
in 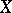 . Examples: an isotone operator, i.e. an operator such that
. Examples: an isotone operator, i.e. an operator such that 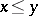 implies
implies 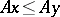 .
.
References
| [1] | L.A. Lyusternik, V.I. Sobolev, "Elemente der Funktionalanalysis" , Akademie Verlag (1955) (Translated from Russian) |
| [2] | W. Rudin, "Functional analysis" , McGraw-Hill (1973) |
| [3] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1967) |
Comments
References
| [a1] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) |
| [a2] | A.C. Zaanen, "Riesz spaces" , II , North-Holland (1983) |
Bounded operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bounded_operator&oldid=17165