Boundary value problems of analytic function theory
Problems of finding an analytic function in a certain domain from a given relation between the boundary values of its real and its imaginary part. This problem was first posed by B. Riemann in 1857 [1]. D. Hilbert [2] studied the boundary value problem formulated as follows (the Riemann–Hilbert problem): To find the function 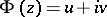 that is analytic in a simply-connected domain
that is analytic in a simply-connected domain 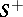 bounded by a contour
bounded by a contour 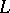 and that is continuous in
and that is continuous in 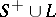 , from the boundary condition
, from the boundary condition
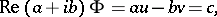 | (1) |
where 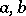 and
and  are given real continuous functions on
are given real continuous functions on 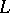 . Hilbert initially reduced this problem to a singular integral equation in order to give an example of the application of such an equation.
. Hilbert initially reduced this problem to a singular integral equation in order to give an example of the application of such an equation.
The problem (1) may be reduced to a successive solution of two Dirichlet problems. A complete study of the problem by this method may be found in [3].
The problem arrived at by H. Poincaré [4] in developing the mathematical theory of tide resembles problem (1). Poincaré's problem consists in determining a harmonic function 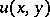 in a domain
in a domain 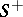 from the following condition on the boundary
from the following condition on the boundary 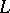 of this domain:
of this domain:
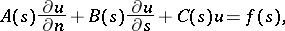 | (2) |
where 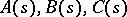 and
and 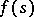 are real functions given on
are real functions given on 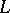 ,
,  is the arc abscissa and
is the arc abscissa and  is the normal to
is the normal to 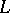 .
.
The generalized Riemann–Hilbert–Poincaré problem is the following linear boundary value problem: To find an analytic function 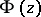 in
in 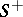 from the boundary condition
from the boundary condition
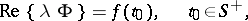 | (3) |
where 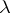 is an integro-differential operator defined by the formula
is an integro-differential operator defined by the formula
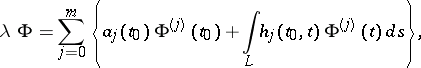 | (4) |
where 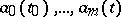 are (usually complex-valued) functions of class
are (usually complex-valued) functions of class  defined on
defined on 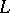 (i.e. satisfying a Hölder condition),
(i.e. satisfying a Hölder condition), 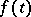 is a given real-valued function of class
is a given real-valued function of class  and
and 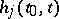 are (usually complex-valued) functions on
are (usually complex-valued) functions on 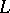 of the form
of the form
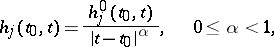 |
where 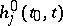 are functions of class
are functions of class 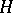 in both variables. The expression
in both variables. The expression 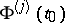 on the right-hand side of (4) is understood to mean the boundary value on
on the right-hand side of (4) is understood to mean the boundary value on 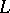 from inside the domain
from inside the domain 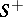 of the
of the 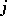 -th order derivative of
-th order derivative of 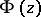 .
.
A special case of the Riemann–Hilbert–Poincaré problem, in the case when 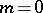 ,
, 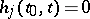 , is the Riemann–Hilbert problem; Poincaré's problem is also a special formulation of the same problem. Many important boundary value problems — such as boundary value problems for partial differential equations of elliptic type with two independent variables — may be reduced to the Riemann–Hilbert–Poincaré problem.
, is the Riemann–Hilbert problem; Poincaré's problem is also a special formulation of the same problem. Many important boundary value problems — such as boundary value problems for partial differential equations of elliptic type with two independent variables — may be reduced to the Riemann–Hilbert–Poincaré problem.
The Riemann–Hilbert–Poincaré problem was also posed for 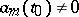 ,
, 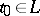 , and was solved by I.N. Vekua [3].
, and was solved by I.N. Vekua [3].
An important role in the theory of boundary value problems is played by the concept of the index of the problem — an integer defined by the formula
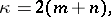 |
where 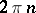 is the increment of
is the increment of 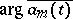 under one complete traversal of the contour
under one complete traversal of the contour 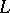 in the direction leaving the domain
in the direction leaving the domain 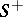 at the left.
at the left.
The Riemann–Hilbert–Poincaré problem is reduced to a singular integral equation of the form
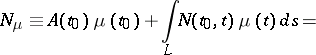 | (5) |
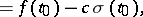 |
where 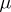 is the unknown real-valued function of class
is the unknown real-valued function of class 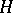 ,
,  is an unknown real constant, and
is an unknown real constant, and
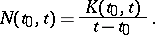 |
The functions 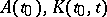 and
and 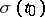 are expressed in terms of
are expressed in terms of 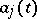 and
and 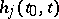 ,
, 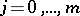 .
.
Let 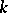 and
and 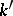 be the numbers of linearly independent solutions of the homogeneous integral equation
be the numbers of linearly independent solutions of the homogeneous integral equation 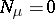 corresponding to (5) and of the homogeneous integral equation
corresponding to (5) and of the homogeneous integral equation
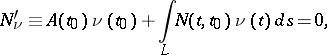 | (6) |
associated with it. The numbers 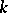 and
and 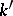 are connected with the index
are connected with the index 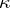 of the Riemann–Hilbert–Poincaré problem by the equality
of the Riemann–Hilbert–Poincaré problem by the equality
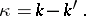 |
Of special interest is the case when the problem is solvable whatever the right-hand side 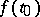 . In order for the Riemann–Hilbert–Poincaré problem to be solvable whatever the right-hand side
. In order for the Riemann–Hilbert–Poincaré problem to be solvable whatever the right-hand side 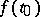 , a necessary and sufficient condition is
, a necessary and sufficient condition is  or
or  , and in the latter case the solution
, and in the latter case the solution 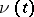 of equation (6) must satisfy the condition
of equation (6) must satisfy the condition
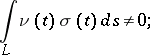 |
in both cases 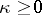 and the homogeneous problem
and the homogeneous problem 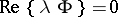 has exactly
has exactly 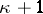 linearly independent solutions. If
linearly independent solutions. If 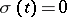 , then the Riemann–Hilbert–Poincaré problem is solvable for any right-hand side if and only if
, then the Riemann–Hilbert–Poincaré problem is solvable for any right-hand side if and only if  .
.
As regards the Riemann–Hilbert problem, the following statements are valid: 1) If 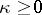 , then the inhomogeneous problem (1) is solvable whatever its right-hand side; and 2) if
, then the inhomogeneous problem (1) is solvable whatever its right-hand side; and 2) if 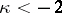 , then the problem has a solution if and only if
, then the problem has a solution if and only if
 |
where
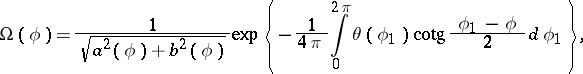 |
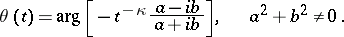 |
The Riemann–Hilbert problem is closely connected with the so-called problem of linear conjugation. Let 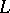 be a smooth or a piecewise-smooth curve consisting of closed contours enclosing some domain
be a smooth or a piecewise-smooth curve consisting of closed contours enclosing some domain 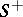 of the complex plane
of the complex plane 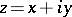 , which remains on the left during traversal of
, which remains on the left during traversal of 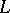 , and let the complement of
, and let the complement of 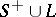 in the
in the  -plane be denoted by
-plane be denoted by 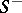 . Let a function
. Let a function 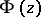 be given, and let it be continuous in a neighbourhood of the curve
be given, and let it be continuous in a neighbourhood of the curve 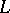 , everywhere except perhaps on
, everywhere except perhaps on 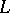 itself. One says that the function
itself. One says that the function 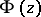 is continuously extendable to a point
is continuously extendable to a point 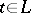 from the left (or from the right) if
from the left (or from the right) if 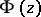 tends to a definite limit
tends to a definite limit 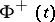 (or
(or 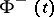 ) as
) as  tends to
tends to 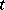 along an arbitrary path, while remaining to the left (or to the right) of
along an arbitrary path, while remaining to the left (or to the right) of 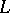 .
.
The function  is said to be piecewise analytic with jump curve
is said to be piecewise analytic with jump curve 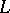 if it is analytic in
if it is analytic in 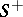 and
and 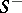 and is continuously extendable to any point
and is continuously extendable to any point  both from the left and from the right.
both from the left and from the right.
The linear conjugation problem consists of determining a piecewise-analytic function  with jump curve
with jump curve 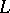 , having finite order at infinity, from the boundary condition
, having finite order at infinity, from the boundary condition
 |
where 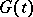 and
and 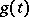 are functions of class
are functions of class 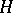 given on
given on 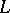 . On the assumption that
. On the assumption that 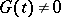 everywhere on
everywhere on 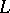 , the integer
, the integer
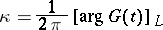 |
is called the index of the linear conjugation problem.
If 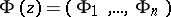 is a piecewise-analytic vector,
is a piecewise-analytic vector, 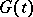 is a square
is a square 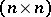 -matrix and
-matrix and 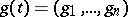 is a vector, and if also
is a vector, and if also 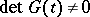 , then the integer
, then the integer
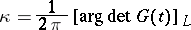 |
is called the total index of the linear conjugation problem. The concepts of the index and the total index play an important role in the theory of the linear conjugation problem [5], [6], [7].
The theory of one-dimensional singular integral equations of the form (5) was constructed on the basis of the theory of the linear conjugation problem.
References
| [1] | B. Riemann, , Gesammelte math. Werke - Nachträge , Teubner (1892–1902) (Translated from German) |
| [2] | D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) |
| [3] | I.N. Vekua, Trudy Tbil. Mat. Inst. Akad. Nauk GruzSSR , 11 (1942) pp. 109–139 |
| [4] | H. Poincaré, "Leçons de mécanique celeste" , 3 , Paris (1910) |
| [5] | N.I. Muskhelishvili, "Singular integral equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [6] | F.D. Gakhov, "Boundary value problems" , Pergamon (1966) (Translated from Russian) |
| [7] | B.V. Khvedelidze, Trudy Tbil. Mat. Inst. Akad. Nauk GruzSSR , 23 (1956) pp. 3–158 |
Comments
The problem discussed in the article is also known as the barrier problem. For applications in mathematical physics, see [a6], [a7], [a9], and the references given there. An important contribution to the theory (matrix case) was given in [a5]. Other relevant publications are [a1], [a2], [a3], [a4] and [a8]. The method proposed in [a1] employs the state space approach from systems theory.
Note that the various names given to various variants of these problems are by no means fixed. Thus, what is called the linear conjugation problem above is also often known as the Riemann–Hilbert problem [a9]. This version, especially the matrix case where 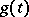 ,
, 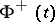 ,
,  are all (invertible) matrix-valued functions, is of great importance in the theory of completely-integrable systems. Indeed, consider an overdetermined system of linear partial differential equations (cf. [a6] for more detail)
are all (invertible) matrix-valued functions, is of great importance in the theory of completely-integrable systems. Indeed, consider an overdetermined system of linear partial differential equations (cf. [a6] for more detail)
 | (a1) |
where 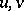 are to be thought of as rational functions in a complex parameter
are to be thought of as rational functions in a complex parameter 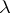 with coefficients depending on
with coefficients depending on 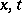 but with the pole structure independent of
but with the pole structure independent of 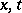 ; e.g.
; e.g.
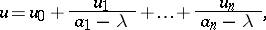 |
with the 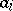 constants and the
constants and the 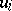 functions of
functions of 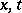 only. An invertible matrix solution
only. An invertible matrix solution 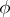 of (a1) exists if and only if the corresponding
of (a1) exists if and only if the corresponding 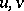 satisfy
satisfy
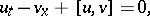 | (a2) |
a so-called Zakharov–Shabat system. Many integrable systems can be put in this form. Now let 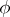 solve (a1) and take a function
solve (a1) and take a function 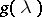 on a contour
on a contour 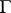 in the
in the 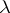 -plane. Solve the
-plane. Solve the 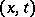 -family of matrix Riemann–Hilbert problems
-family of matrix Riemann–Hilbert problems 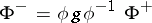 . Then
. Then 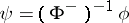 also solves (a1) and this leads to an action of the group of invertible matrix-valued functions in
also solves (a1) and this leads to an action of the group of invertible matrix-valued functions in 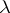 on the space of solutions of (a2). This method of obtaining a new solution
on the space of solutions of (a2). This method of obtaining a new solution 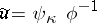 ,
, 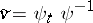 from an old one
from an old one 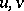 and a function
and a function 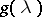 is known as the Zakharov–Shabat dressing method.
is known as the Zakharov–Shabat dressing method. 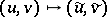 is also sometimes known as a Riemann–Hilbert transformation. In the case of Einstein's field equations (axisymmetric solutions) a similar technique goes by the names of Hauser–Ernst or Kinnersley–Chitre transformations, and in that case (a subgroup of) the group involved is known as the Geroch group [a10]. The Riemann monodromy problem asks for
is also sometimes known as a Riemann–Hilbert transformation. In the case of Einstein's field equations (axisymmetric solutions) a similar technique goes by the names of Hauser–Ernst or Kinnersley–Chitre transformations, and in that case (a subgroup of) the group involved is known as the Geroch group [a10]. The Riemann monodromy problem asks for  multi-valued functions
multi-valued functions 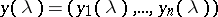 regular everywhere but in
regular everywhere but in 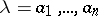 ,
, 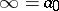 , such that analytic continuation around a contour containing exactly one of these points changes
, such that analytic continuation around a contour containing exactly one of these points changes 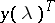 into
into 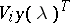 ,
, 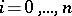 . This problem reduces to the Riemann–Hilbert problem by taking a contour through
. This problem reduces to the Riemann–Hilbert problem by taking a contour through  and a suitable step function on it. The Riemann monodromy problem was essentially solved by J. Plemelj [a11], G.D. Birkhoff , and I.A. Lappo-Danilevsky [a13].
and a suitable step function on it. The Riemann monodromy problem was essentially solved by J. Plemelj [a11], G.D. Birkhoff , and I.A. Lappo-Danilevsky [a13].
References
| [a1] | H. Bart, I. Gohberg, M.A. Kaashoek, "Fredholm theory of Wiener–Hopf equations in terms of realization of their symbols" Integral Equations and Operator Theory , 8 (1985) pp. 590–613 |
| [a2] | "Mathématique et physique" L. Boutet de Monvel (ed.) et al. (ed.) , Sem. ENS 1979–1982 , Birkhäuser (1983) |
| [a3] | K. Clancey, I. Gohberg, "Factorization of matrix functions and singular integral operators" , Operator Theory: Advances and Applications , 3 , Birkhäuser (1981) |
| [a4] | I.C. [I.Ts. Gokhberg] Gohberg, I.A. Feld'man, "Convolution equations and projection methods for their solution" , Transl. Math. Monogr. , 41 , Amer. Math. Soc. (1974) (Translated from Russian) |
| [a5] | I.C. Gohberg, M.G. Krein, "Systems of integral equations on a half line with kernels depending on the difference of arguments" Amer. Math. Soc. Transl. (2) (1960) pp. 217–287 Uspekhi Mat. Nauk , 13 : 2 (80) (1958) pp. 3–72 |
| [a6] | V.E. Zakharov, S.V. Manakov, "Soliton theory" J.M. Khalatnikov (ed.) , Physics reviews , 1 , Harwood Acad. Publ. (1979) pp. 133–190 |
| [a7] | E. Meister, "Randwertaufgaben der Funktionentheorie" , Teubner (1983) |
| [a8] | Yu.L. Rodin, "The Riemann boundary value problem on Riemannian manifolds" , Reidel (1988) (Translated from Russian) |
| [a9] | D.V. Chudnovsky (ed.) G. Chudnovsky (ed.) , The Riemann problem, complete integrability and arithmetic applications , Lect. notes in math. , 925 , Springer (1982) |
| [a10] | C. Hoenselaers, W. Dietz, "Solutions of Einstein's equations: techniques and results" , Lect. notes in physics , 265 , Springer (1984) |
| [a11] | J. Plemelj, "Problems in the sense of Riemann and Klein" , Interscience (1964) |
| [a12a] | G.D. Birkhoff, "Singular points of ordinary linear differential equations" Trans. Amer. Math. Soc. , 10 (1909) pp. 436–470 |
| [a12b] | G.D. Birkhoff, "A simplified treatment of the regular singular point" Trans. Amer. Math. Soc. , 11 (1910) pp. 199–202 |
| [a13] | I.A. Lappo-Danilevsky, "Mémoire sur la théorie des systèmes des équations différentielles linéaires" , Chelsea, reprint (1953) |
Boundary value problems of analytic function theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_value_problems_of_analytic_function_theory&oldid=13982