Boundary value problems in potential theory
Fundamental problems in both classical and abstract potential theory. The classical Newton and logarithmic potentials satisfy certain partial differential equations of elliptic type: the Laplace equation in regions free of the masses generating the potentials, and the Poisson equation in regions occupied by the masses. It follows, therefore, that the boundary value problems of potential theory are primarily boundary value problems for elliptic equations and systems (cf. Boundary value problem, elliptic equations).
1) The Dirichlet problem, or first boundary value problem. Here the problem is to find a potential  in some domain
in some domain  , given its continuous restriction
, given its continuous restriction  ,
,  , to the boundary
, to the boundary  of the domain on the assumption that the mass distribution in the interior of
of the domain on the assumption that the mass distribution in the interior of  is known. This is a fundamental problem in potential theory.
is known. This is a fundamental problem in potential theory.
2) The Neumann problem, or second boundary value problem. Here the problem is to find a potential in  , given the continuous restriction of its normal derivative
, given the continuous restriction of its normal derivative
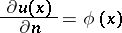 |
to  .
.
3) The mixed problem, or third boundary value problem. Here the known data on  constitute a linear combination
constitute a linear combination
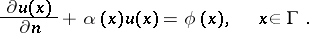 | (*) |
4) The problem with oblique derivative arises when the normal derivative 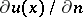 in condition (*) is replaced by the derivative
in condition (*) is replaced by the derivative  with respect to an arbitrary direction
with respect to an arbitrary direction  ,
, 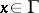 .
.
In addition to these general problems, the following specific problems have also arisen in potential theory.
5) The Robin problem. Here it is required to find a mass distribution on 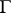 with a constant potential in the interior of
with a constant potential in the interior of  . This problem appears in electrostatics, when it is required to determine an equilibrium charge distribution on a conductor
. This problem appears in electrostatics, when it is required to determine an equilibrium charge distribution on a conductor  which has no effect anywhere inside
which has no effect anywhere inside  .
.
6) The balayage method, which, in its simplest presentation dating back to H. Poincaré, amounts to finding a "swept-out" mass distribution on 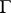 the potential of which in the complementary domain
the potential of which in the complementary domain 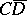 coincides with the potential of given masses in the interior of
coincides with the potential of given masses in the interior of  . The two last problems are particularly important in abstract potential theory (see Potential theory, abstract). See also Bessel potential; Non-linear potential; Riesz potential.
. The two last problems are particularly important in abstract potential theory (see Potential theory, abstract). See also Bessel potential; Non-linear potential; Riesz potential.
References
| [1] | N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from French) |
| [2] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [3] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
| [4] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
Comments
Well-known additional references are [a1], [a2], [a3]. Boundary value problems for parabolic equations can be considered in the same way as those in potential theory, cf. [a3]. The relation between boundary value problems and the theory of Markov processes is considered in [a3].
References
| [a1] | O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967) |
| [a2] | L.L. Helms, "Introduction to potential theory" , Wiley (Interscience) (1969) |
| [a3] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1983) |
Boundary value problems in potential theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_value_problems_in_potential_theory&oldid=18939