Difference between revisions of "Boundary properties of analytic functions"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b0173301.png | ||
| + | $#A+1 = 263 n = 3 | ||
| + | $#C+1 = 263 : ~/encyclopedia/old_files/data/B017/B.0107330 Boundary properties of analytic functions | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
Properties of analytic functions that are displayed as the function approaches the boundary of its domain of definition. | Properties of analytic functions that are displayed as the function approaches the boundary of its domain of definition. | ||
It can be said that the study of boundary properties of analytic functions, understood in the widest sense of the word, began with the [[Sokhotskii theorem|Sokhotskii theorem]] and the [[Picard theorem|Picard theorem]] about the behaviour of analytic functions in a neighbourhood of isolated essential singular points (cf. [[Essential singular point|Essential singular point]]), which were obtained in the second half of the 19th century. The terms relevant to this approach to the study of boundary properties of analytic functions — which is now called the theory of prime ends and cluster sets (cf. [[Limit elements|Limit elements]]) — first appeared in a course given by P. Painlevé in 1895. The dissertation of P. Fatou (1906) is the first systematic study of certain boundary properties of analytic functions in a neighbourhood of the continuous boundary of their domain of definition. The theory of boundary properties made considerable advances in the first third of the 20th century, owing to the work of several scientists; it resumed its rapid advance in the second half of that century, accompanied by the appearance of new ideas and methods, novel directions and objects of study. Its development is closely connected with various fields of mathematical analysis and mathematics in general, first and foremost with probability theory, the theory of harmonic functions, the theory of conformal mapping, boundary value problems of analytic function theory, potential theory, value-distribution theory, Riemann surfaces, subharmonic functions and function algebras. The theory of boundary properties of analytic functions is closely connected with various fields of application of mathematics by way of boundary value problems. | It can be said that the study of boundary properties of analytic functions, understood in the widest sense of the word, began with the [[Sokhotskii theorem|Sokhotskii theorem]] and the [[Picard theorem|Picard theorem]] about the behaviour of analytic functions in a neighbourhood of isolated essential singular points (cf. [[Essential singular point|Essential singular point]]), which were obtained in the second half of the 19th century. The terms relevant to this approach to the study of boundary properties of analytic functions — which is now called the theory of prime ends and cluster sets (cf. [[Limit elements|Limit elements]]) — first appeared in a course given by P. Painlevé in 1895. The dissertation of P. Fatou (1906) is the first systematic study of certain boundary properties of analytic functions in a neighbourhood of the continuous boundary of their domain of definition. The theory of boundary properties made considerable advances in the first third of the 20th century, owing to the work of several scientists; it resumed its rapid advance in the second half of that century, accompanied by the appearance of new ideas and methods, novel directions and objects of study. Its development is closely connected with various fields of mathematical analysis and mathematics in general, first and foremost with probability theory, the theory of harmonic functions, the theory of conformal mapping, boundary value problems of analytic function theory, potential theory, value-distribution theory, Riemann surfaces, subharmonic functions and function algebras. The theory of boundary properties of analytic functions is closely connected with various fields of application of mathematics by way of boundary value problems. | ||
| − | Since the study of boundary properties is connected, in the first place, with the geometry of the boundary | + | Since the study of boundary properties is connected, in the first place, with the geometry of the boundary $ \Gamma $ |
| + | of the domain of definition $ D $ | ||
| + | of an analytic function $ f(z) $ | ||
| + | in one complex variable $ z $, | ||
| + | three main approaches can be distinguished in the theory of boundary properties of analytic functions. | ||
| − | a) The study of the behaviour of | + | a) The study of the behaviour of $ f(z) $ |
| + | in a neighbourhood of an isolated boundary point $ a \in \Gamma $. | ||
| + | The most important case is that of an essential singular point $ a $, | ||
| + | which is dealt with in the theorems of Sokhotskii, Picard, Julia, and Iversen (cf. [[Sokhotskii theorem|Sokhotskii theorem]]; [[Picard theorem|Picard theorem]]; [[Julia theorem|Julia theorem]]; [[Iversen theorem|Iversen theorem]]). | ||
| − | b) The study of the behaviour of | + | b) The study of the behaviour of $ f(z) $ |
| + | in the case when the boundary $ \Gamma $ | ||
| + | is an everywhere-discontinuous set. V.V. Golubev's dissertation Single-valued analytic functions with a perfect set of singular points (1916, cf. [[#References|[1]]]) was of great importance in this connection. | ||
| − | c) The study of the behaviour of | + | c) The study of the behaviour of $ f(z) $ |
| + | when the domain $ D $ | ||
| + | is bounded by a continuous closed curve $ \Gamma $ | ||
| + | and, in particular, by the unit circle. | ||
Cases a) and c) are, in a sense, extreme cases, while case b) is intermediate. Case c), which is discussed below, has been the subject of most intense study. | Cases a) and c) are, in a sense, extreme cases, while case b) is intermediate. Case c), which is discussed below, has been the subject of most intense study. | ||
| − | Let an analytic function | + | Let an analytic function $ f(z) $ |
| + | be defined in a finite simply-connected domain $ D $ | ||
| + | of the complex $ z $- | ||
| + | plane bounded by a rectifiable Jordan curve $ \Gamma $. | ||
| + | The following problems are fundamental in the classical approach to the study of boundary properties of analytic functions. | ||
| + | |||
| + | 1) The problem of the existence of boundary values, i.e. the question under which conditions and in which sense the boundary values of $ f(z) $ | ||
| + | exist as the point $ z $ | ||
| + | approaches $ \Gamma $. | ||
| + | This problem, as well as the succeeding ones, can be formulated in a different manner as the problem of identifying sufficiently extensive classes of analytic functions in $ D $ | ||
| + | that have, in some sense, boundary values for sufficiently large sets of points on $ \Gamma $. | ||
| + | |||
| + | 2) The problem of boundary representation of $ f(z) $, | ||
| + | i.e. the problem under which conditions and with what kind of analytic apparatus the dependence of $ f(z) $ | ||
| + | on its boundary values on $ \Gamma $ | ||
| + | can be expressed. Clearly, this apparatus will be different for different classes of analytic functions. | ||
| + | |||
| + | 3) The uniqueness problem, or the problem of the properties that a set $ E \subset \Gamma $ | ||
| + | should have such that two analytic functions of a given class coincide in $ D $ | ||
| + | if their boundary values on $ E $ | ||
| + | are identical. | ||
| + | |||
| + | The first result in the solution of the existence problem is the theorem of Fatou (1906): If an analytic function is bounded in the unit disc $ D = \{ {z } : {| z | < 1 } \} $, | ||
| + | $ | f(z) | \leq M $, | ||
| + | then radial boundary, or limit, values $ f(e ^ {i \theta } ) = \lim\limits _ {r \rightarrow 1 - 0 } f (re ^ {i \theta } ) $ | ||
| + | exist almost everywhere with respect to the Lebesgue measure on the unit circle $ \Gamma = \{ {z } : {| z | = 1 } \} $. | ||
| + | It can be shown that, under these conditions, not only radial, but also angular boundary values, or boundary values along all non-tangential paths, exist almost everywhere on $ \Gamma $. | ||
| + | This means that, for almost-all points $ e ^ {i \theta } \in \Gamma $, | ||
| + | $ f(z) $ | ||
| + | tends to a definite limit $ f ( e ^ {i \theta } ) $ | ||
| + | as $ z $ | ||
| + | tends to the point $ e ^ {i \theta } $ | ||
| + | while remaining within an arbitrary fixed angle | ||
| − | + | $$ | |
| + | \Delta (e ^ {i \theta } , \epsilon ) = \ | ||
| + | \{ | z | < 1 \} \cap | ||
| + | \left \{ | \mathop{\rm arg} (e ^ {i \theta } - z) | < | ||
| + | { | ||
| + | \frac \pi {2} | ||
| + | } - \epsilon \right \} , | ||
| + | $$ | ||
| − | 2 | + | $ \epsilon > 0 $, |
| + | of width $ \pi - 2 \epsilon < \pi $, | ||
| + | with apex at the point $ e ^ {i \theta } $, | ||
| + | bisected by the radius drawn through the point $ e ^ {i \theta } $. | ||
| + | Fatou's theorem cannot, in a certain sense, be improved upon; it was in fact shown by N.N. Luzin (1919) that for any set $ E \subset \Gamma $ | ||
| + | of measure zero on $ \Gamma $ | ||
| + | there exists a bounded analytic function $ f(z) $ | ||
| + | not having radial limits on $ E $. | ||
| − | + | The class of bounded analytic functions in a domain $ D $ | |
| + | is denoted by $ B(D) $ | ||
| + | or $ H ^ \infty (D) $. | ||
| + | Following the results of Fatou, the next problem appeared to be the generalization of his theorems to wider classes of functions. One distinguishes between the following basic classes of functions in the unit disc $ D $, | ||
| + | which are related by proper inclusions: | ||
| − | + | $$ \tag{1 } | |
| + | A (D) \subset B (D) = H ^ \infty (D) \subset \ | ||
| + | H ^ {p} (D) \subset N ^ {*} (D) \subset N (D). | ||
| + | $$ | ||
| − | + | The class $ A(D) $ | |
| + | is the class of single-valued analytic functions in $ D $ | ||
| + | that are continuous in the closed domain $ D \cup \Gamma = \overline{D}\; $. | ||
| − | + | The classes $ H ^ {p} (D) $, | |
| + | for all positive numbers $ p $, | ||
| + | are defined by the condition | ||
| − | + | $$ \tag{2 } | |
| + | \| f \| _ {p} = \ | ||
| + | \sup _ {0 < r < 1 } \ | ||
| + | \left \{ | ||
| + | \frac{1}{2 \pi } | ||
| + | \int\limits _ { 0 } ^ { {2 } \pi } | ||
| + | | f (re ^ {i \phi } ) | ^ {p} \ | ||
| + | d \phi \right \} ^ {1/p} = \ | ||
| + | C (f, p) < | ||
| + | $$ | ||
| − | < | + | $$ |
| + | < \ | ||
| + | + \infty . | ||
| + | $$ | ||
| − | The | + | The proper inclusions $ H ^ \infty \subset H ^ {p _ {1} } \subset H ^ {p _ {2} } $ |
| + | are valid for any $ 0 < p _ {1} < p _ {2} < + \infty $. | ||
| + | The classes $ H ^ {p} $ | ||
| + | were first introduced by G.H. Hardy (1915), and are often named Hardy classes. If $ 1 \leq p < \infty $, | ||
| + | one can introduce the norm (2) on $ H ^ {p} $, | ||
| + | and the norm | ||
| − | + | $$ | |
| + | \| f \| _ \infty = \ | ||
| + | \| f \| _ {B} = \ | ||
| + | \sup _ {z \in D } \ | ||
| + | | f(z) | | ||
| + | $$ | ||
| − | + | on $ H ^ \infty $; | |
| + | the classes $ H ^ {p} $, | ||
| + | $ 1 \leq p \leq + \infty $, | ||
| + | have a natural structure of a vector space, and become Banach Hardy spaces. If $ 0 < p < 1 $, | ||
| + | it is only possible to introduce the metric $ \rho _ {p} (f, g) = \| f - g \| _ {p} ^ {p} $ | ||
| + | on $ H ^ {p} $, | ||
| + | which converts the latter into a complete metric non-normable space. The class of bounded analytic functions $ B = H ^ \infty $ | ||
| + | is contained in any class $ H ^ {p} $, | ||
| + | $ p > 0 $. | ||
| − | + | The class $ N(D) $ | |
| + | of certain meromorphic functions $ f(z) $ | ||
| + | in the unit disc $ D $ | ||
| + | is said to be the class of functions of bounded characteristic; it was introduced in 1924 by R. Nevanlinna. The class $ N(D) $ | ||
| + | can be characterized as the set of meromorphic functions $ f(z) $ | ||
| + | in $ D $ | ||
| + | that can be represented as the ratio of two bounded regular functions $ f _ {1} (z) $ | ||
| + | and $ f _ {2} (z) $ | ||
| + | in $ D $, | ||
| + | $ f(z) = f _ {1} (z)/f _ {2} (z) $. | ||
| − | + | All regular functions $ f(z) \in N(D) $ | |
| + | form a subclass $ N ^ {*} (D) $, | ||
| + | and $ f(z) \in N ^ {*} (D) $ | ||
| + | if and only if the condition | ||
| − | + | $$ \tag{3 } | |
| + | \sup _ {0 < r < 1 } \ | ||
| − | + | \frac{1}{2 \pi } | |
| + | \int\limits _ { 0 } ^ { {2 } \pi } | ||
| + | \mathop{\rm ln} ^ {+} | f (re ^ {i \phi } ) | \ | ||
| + | d \phi = C (f) < + \infty , | ||
| + | $$ | ||
| − | + | where $ \mathop{\rm ln} ^ {+} x = \mathop{\rm ln} x $ | |
| + | if $ \mathop{\rm ln} x \geq 0 $ | ||
| + | and $ \mathop{\rm ln} ^ {+} x = 0 $ | ||
| + | if $ \mathop{\rm ln} x < 0 $, | ||
| + | is fulfilled. The class $ N ^ {*} (D) $ | ||
| + | contains all classes $ H ^ {p} $, | ||
| + | $ 0 < p \leq + \infty $. | ||
| − | + | The classes $ H ^ {p} $ | |
| + | have the following generalization. Let $ \psi (t) $ | ||
| + | be a strictly-convex function for $ - \infty < t < + \infty $, | ||
| + | i.e. a non-negative, convex, non-decreasing function such that $ \psi (t) / t \rightarrow + \infty $ | ||
| + | as $ t \rightarrow + \infty $. | ||
| + | The class $ H _ \psi (D) $ | ||
| + | is then defined by the condition | ||
| − | + | $$ \tag{2'} | |
| + | \sup _ {0 < r < 1 } \ | ||
| + | \psi ^ {-1} \left \{ | ||
| + | \frac{1}{2 \pi } | ||
| − | + | \int\limits _ { 0 } ^ { {2 } \pi } \psi | |
| + | ( \mathop{\rm ln} | f (re ^ {i \phi } ) | ) d \phi \right \} = \ | ||
| + | C (f, \psi ) < | ||
| + | $$ | ||
| − | + | $$ | |
| + | < \ | ||
| + | + \infty , | ||
| + | $$ | ||
| − | + | compare with condition (2), where $ \psi (t) = e ^ {pt} $. | |
| − | + | The principal result obtained for the problem of the existence of boundary values in the case of the unit disc $ D $ | |
| + | states that each meromorphic function $ f (z) $ | ||
| + | of bounded characteristic in $ D $ | ||
| + | has angular boundary values $ f (e ^ {i \theta } ) $ | ||
| + | almost everywhere on $ \Gamma $; | ||
| + | these boundary values are such that the function $ \mathop{\rm ln} | f ( e ^ {i \theta } ) | $ | ||
| + | is Lebesgue integrable on $ \Gamma $. | ||
| + | The following additional property is displayed by the classes $ H ^ {p} $, | ||
| + | $ 0 < p < + \infty $, | ||
| + | or $ H _ \psi $: | ||
| + | The function $ | f (e ^ {i \theta } ) | ^ {p} $ | ||
| + | or, correspondingly, $ \psi ( \mathop{\rm ln} | f ( e ^ {i \theta } ) | ) ^ {p} $ | ||
| + | is Lebesgue integrable on $ \Gamma $. | ||
| + | For bounded functions $ f(z) $, | ||
| + | $ | f(z) | \leq M $, | ||
| + | one has instead of the above, $ \mathop{\rm esssup} | f (e ^ {i \theta } ) | \leq M $, | ||
| + | $ 0 \leq \theta \leq 2 \pi $. | ||
| + | Thus, condition (3) is the widest sufficient condition on the average increase of an analytic function $ f(z) $, | ||
| + | as $ | z | \rightarrow 1 $, | ||
| + | that ensures the existence of angular boundary values almost everywhere on $ \Gamma $. | ||
| − | + | It has been shown that condition (3) cannot be substantially weakened. Thus, it was shown by A. Zygmund that for an arbitrary increasing function $ \psi (t) $, | |
| + | $ \psi (t) / t \rightarrow 0 $ | ||
| + | as $ 0 < t \uparrow + \infty $, | ||
| + | there exists an analytic function $ f(z) $ | ||
| + | in $ D $ | ||
| + | such that | ||
| − | + | $$ | |
| + | \sup _ {0 < r < 1 } \ | ||
| + | \int\limits _ { 0 } ^ { {2 } \pi } \psi | ||
| + | ( \mathop{\rm ln} ^ {+} | f (re ^ {i \phi } ) | ) \ | ||
| + | d \phi < + \infty , | ||
| + | $$ | ||
| − | + | but which has no boundary values anywhere on $ \Gamma $. | |
| + | Even if the maximum $ M (r; f) = \max \{ {| f(z) | } : {| z | = r } \} $ | ||
| + | grows as slowly as one pleases, there still exist analytic functions without radial boundary values. | ||
| − | + | The boundary representation of functions $ f(z) $ | |
| + | of class $ N(D) $, | ||
| + | characterizing the functions of this class, has the form | ||
| − | + | $$ \tag{4 } | |
| + | f (z) = z ^ {m} e ^ {i \lambda } | ||
| − | + | \frac{B _ {1} (z; a _ \mu ) }{B _ {2} (z; b _ \nu ) } | |
| + | \times | ||
| + | $$ | ||
| − | + | $$ | |
| + | \times | ||
| + | \mathop{\rm exp} | ||
| + | \frac{1}{2 \pi } | ||
| + | \int\limits _ { 0 } ^ { {2 } \pi } \mathop{\rm ln} | ||
| + | | f (e ^ {i \theta } ) | | ||
| + | \frac{e ^ {i \theta } | ||
| + | + z }{e ^ {i \theta } - z } | ||
| + | d \theta \times | ||
| + | $$ | ||
| − | + | $$ | |
| + | \times | ||
| + | \mathop{\rm exp} | ||
| + | \frac{1}{2 \pi } | ||
| + | \int\limits _ { 0 } ^ { {2 } \pi } | ||
| + | \frac{e ^ {i \theta } + z }{e ^ {i \theta } - z } | ||
| + | d \Phi ( \theta ), | ||
| + | $$ | ||
| − | + | where $ m $ | |
| + | is an integer, $ m = k $ | ||
| + | if the point $ z = 0 $ | ||
| + | is a zero of multiplicity $ k $ | ||
| + | and $ m = - k $ | ||
| + | if $ z = 0 $ | ||
| + | is a pole of multiplicity $ k $; | ||
| + | $ \lambda $ | ||
| + | is a real number; | ||
| − | + | $$ \tag{5 } | |
| + | B _ {1} (z; a _ \mu ) = \ | ||
| + | \prod _ {\mu = 1 } ^ \infty | ||
| − | + | \frac{| a _ \mu | }{a _ \mu } | |
| − | + | \frac{a _ \mu - z }{1 - \overline{ {a _ \mu }}\; z } | |
| − | + | $$ | |
| − | + | is the [[Blaschke product|Blaschke product]] taken over all the zeros $ a _ \mu \neq 0 $ | |
| + | of $ f (z) $ | ||
| + | inside $ D $ | ||
| + | taking into account their multiplicity; $ B _ {2} (z; b _ \nu ) $ | ||
| + | is the Blaschke product of type (5) taken over all poles $ b _ \nu \neq 0 $ | ||
| + | of $ f(z) $ | ||
| + | in $ D $; | ||
| + | and $ \Phi ( \theta ) $ | ||
| + | is a singular function of bounded variation on $ [0, 2 \pi ] $ | ||
| + | with a derivative that vanishes almost everywhere. In (4), the last integral is of Lebesgue–Stieltjes type, while the first is of Lebesgue type. | ||
| − | + | It was shown by M.M. Dzhrbashyan [[#References|[10]]] that the theory of meromorphic functions of bounded characteristic can be considerably extended. It is possible, in fact, to introduce a family of classes of meromorphic functions $ N _ \alpha $ | |
| + | depending on a continuous parameter $ \alpha $, | ||
| + | $ -1 < \alpha < + \infty $, | ||
| + | and the classes $ N _ \alpha $ | ||
| + | are characterized by representations yielding (4) when $ \alpha = 0 $. | ||
| + | As $ \alpha $ | ||
| + | increases, the classes $ N _ \alpha $ | ||
| + | become larger, and $ N _ {0} $ | ||
| + | becomes identical with Nevanlinna's class $ N $. | ||
| − | + | For analytic functions $ f(z) \in N ^ {*} (D) $ | |
| + | in the representation (4) one must put $ B _ {2} (z; b _ \nu ) \equiv 1 $. | ||
| + | For the functions $ f(z) \in H ^ {p} $, | ||
| + | $ 0 < p \leq + \infty $, | ||
| + | or $ \in H _ \psi $, | ||
| + | in the representation (4) one has $ B _ {2} (z; b _ \nu ) \equiv 1 $, | ||
| + | and $ \Phi ( \theta ) $ | ||
| + | is a non-increasing function of the indicated type. See also [[Cauchy integral|Cauchy integral]]. | ||
| − | + | The first results in the uniqueness problem were obtained in 1916 by the brothers F. and M. Riesz: If a function $ f(z) \in H ^ \infty $ | |
| + | has radial boundary values $ f (e ^ {i \theta } ) = 0 $ | ||
| + | on a set $ E \subset \Gamma $ | ||
| + | of positive Lebesgue measure on $ \Gamma $, | ||
| + | then $ f(z) \equiv 0 $ | ||
| + | in $ D $. | ||
| + | The representation (4) makes it possible to extend this theorem to meromorphic functions of bounded characteristic (cf. [[Function of bounded form|Function of bounded form]]). N.N. Luzin (1919) constructed, for any set $ E \subset \Gamma $ | ||
| + | of measure zero, an analytic function $ f(z) $ | ||
| + | such that $ f ( e ^ {i \theta } ) = 0 $ | ||
| + | everywhere on $ E $ | ||
| + | as $ z \rightarrow e ^ {i \theta } $ | ||
| + | in an arbitrary manner, but $ f (z) $ | ||
| + | is not identically equal to zero. The deepest and most general boundary uniqueness theorems for meromorphic functions of general form were obtained in 1925 by Luzin and I.I. Privalov (cf. [[Uniqueness properties of analytic functions|Uniqueness properties of analytic functions]]; [[Luzin–Privalov theorems|Luzin–Privalov theorems]]). | ||
| − | + | Consider the case of an arbitrary plane domain $ D $; | |
| + | for the sake of brevity, only simply-connected domains $ D $ | ||
| + | with a rectifiable boundary $ \Gamma $ | ||
| + | will be discussed. The conditions (2), (3) and (2'}) are equivalent to stipulating that the subharmonic functions $ {| f(z) | } ^ {p} $, | ||
| + | $ \mathop{\rm ln} ^ {+} | f(z) | $ | ||
| + | and $ \psi ( \mathop{\rm ln} | f (z) | ) $, | ||
| + | respectively, have a [[Harmonic majorant|harmonic majorant]] in $ D $. | ||
| + | In such a form these conditions are fully suitable, and furnish a natural definition of the classes $ H ^ {p} $, | ||
| + | $ N ^ {*} $ | ||
| + | and $ H _ \psi $ | ||
| + | in arbitrary domains. It is known that a rectifiable curve $ \Gamma $ | ||
| + | has a definite tangent and normal at almost all of its points. The inclusions (1) remain valid, as does Fatou's theorem on the almost-everywhere existence on $ \Gamma $ | ||
| + | of angular boundary values for the class $ N ^ {*} $. | ||
| + | Here, as the bisectrix of the angular domains $ \Delta ( \zeta , \epsilon ) $ | ||
| + | the normal to $ \Gamma $ | ||
| + | at the point $ \zeta \in \Gamma $ | ||
| + | is taken. The Riesz uniqueness theorem for the class $ N ^ {*} $ | ||
| + | is also applicable. | ||
| − | + | V.I. Smirnov also introduced the frequently employed classes $ E ^ {p} $, | |
| + | $ p > 0 $, | ||
| + | for the case of an arbitrary domain $ D $. | ||
| + | These classes have the following definition: $ f(z) \in E ^ {p} (D) $ | ||
| + | if there exist a sequence of contours $ \{ \Gamma _ {j} \} \subset D $, | ||
| + | $ \Gamma _ {j} \rightarrow \Gamma $, | ||
| + | such that | ||
| − | + | $$ | |
| + | \sup _ {\{ \Gamma _ {j} \} } \ | ||
| + | \int\limits _ {\Gamma _ {j} } | ||
| + | | f (z) | ^ {p} | ||
| + | | dz | = C (f, p) < + \infty . | ||
| + | $$ | ||
| − | + | The classes $ E ^ {p} $ | |
| + | are especially convenient in the study of problems of representation of functions in the form of a Cauchy integral. | ||
| − | < | + | Of major interest is the study of the boundary properties of analytic functions realizing a conformal mapping. Let a function $ z = F (w) $ |
| + | realize a conformal mapping of the unit disc $ | w | < 1 $ | ||
| + | onto a domain $ D $ | ||
| + | of the $ z $- | ||
| + | plane with a rectifiable boundary $ \Gamma $. | ||
| + | It has been shown, for example, that in such a case the derivative $ F ^ { \prime } (w) $ | ||
| + | belongs to the Hardy class $ H ^ {1} $ | ||
| + | in the disc $ | w | < 1 $, | ||
| + | so that it is representable in the form (4) with $ B _ {2} \equiv 1 $ | ||
| + | and a non-increasing singular function $ \Phi ( \theta ) $. | ||
| + | Smirnov pointed out the importance of the class $ S $ | ||
| + | of such domains $ D $ | ||
| + | for which this singular function $ \Phi ( \theta ) \equiv 0 $. | ||
| + | In 1937 M.V. Keldysh and M.A. Lavrent'ev constructed an example of a domain with a rectifiable boundary that is not included in the Smirnov classes just mentioned; this renders the characterization of domains of Smirnov type even more important. | ||
| − | + | Numerous workers also attempt to study boundary properties of analytic functions $ f(z) $ | |
| + | in several variables $ z = (z _ {1} \dots z _ {n} ) $. | ||
| + | Let $ D = U ^ {n} = \{ {z \in \mathbf C ^ {n} } : {| z _ {j} | < 1, j = 1 \dots n } \} $ | ||
| + | be the unit [[Polydisc|polydisc]], and let $ T ^ {n} = \{ {z \in \mathbf C ^ {n} } : {| z _ {j} | = 1, j = 1 \dots n } \} $ | ||
| + | be its skeleton. The class $ N ^ {*} (D) $ | ||
| + | of analytic functions $ f(z) $ | ||
| + | in $ D $ | ||
| + | is defined by the condition | ||
| − | < | + | $$ |
| + | \sup _ {0 < r < 1 } \ | ||
| + | \int\limits _ {T ^ {n} } | ||
| + | \mathop{\rm ln} ^ {+} | f(rz) | \ | ||
| + | dm _ {n} (z) = \ | ||
| + | C (f) < + \infty , | ||
| + | $$ | ||
| − | + | which is analogous to (3), while the classes $ H ^ {p} (D) $ | |
| + | or $ H _ \psi (D) $ | ||
| + | by the condition of the type ( $ \psi (t) = e ^ {pt} $ | ||
| + | for the case $ H ^ {p} (D) $, | ||
| + | $ p > 0 $): | ||
| − | Many boundary properties may be applied to various generalizations of analytic functions, in particular to abstract analytic functions | + | $$ |
| + | \sup _ {0 < r < 1 } \ | ||
| + | \psi ^ {-1} | ||
| + | \left \{ \int\limits _ {T ^ {n} } | ||
| + | \psi ( \mathop{\rm ln} | f (rz) |) \ | ||
| + | dm _ {n} (z) \right \} = \ | ||
| + | C(f, \psi ) < + \infty , | ||
| + | $$ | ||
| + | |||
| + | where $ m _ {n} $ | ||
| + | is the normalized [[Haar measure|Haar measure]] on $ T ^ {n} $, | ||
| + | $ m _ {n} (T ^ {n} ) = 1 $. | ||
| + | Inclusions of the type $ B = H ^ \infty \subset H _ \psi \subset N ^ {*} $ | ||
| + | are preserved. Analytic functions $ f(z) \in N ^ {*} (D) $ | ||
| + | have "radial" boundary values $ f ^ {*} (z) = \lim\limits _ {r \rightarrow 1 - 0 } f(rz) $, | ||
| + | $ z \in T ^ {n} $, | ||
| + | almost everywhere on $ T ^ {n} $ | ||
| + | with respect to the Haar measure $ m _ {n} $; | ||
| + | and $ \mathop{\rm ln} ^ {+} | f ^ {*} (z) | $ | ||
| + | is summable on $ T _ {n} $ | ||
| + | with respect to $ m _ {n} $. | ||
| + | Sufficiently simple and general characteristics for boundary representations and uniqueness properties of functions $ f(z) $ | ||
| + | in $ U ^ {n} $ | ||
| + | for $ n > 1 $ | ||
| + | have not yet (1986) been found. | ||
| + | |||
| + | Many boundary properties may be applied to various generalizations of analytic functions, in particular to abstract analytic functions $ f: D \rightarrow X $, | ||
| + | which have values in, say, a separable locally convex topological space $ X $ | ||
| + | over the field $ \mathbf C $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.V. Golubev, "Univalent analytic functions. Automorphic functions" , Moscow (1961) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.Ya. Khavinson, "Analytic functions of bounded type" ''Itogi Nauk. Mat. Anal. 1963'' (1965) pp. 5–80 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Noshiro, "Cluster sets" , Springer (1960)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.R. MacLane, "Asymptotic values of holomorphic functions" , ''Rice Univ. Studies, Math. Monographs'' , '''49''' : 1 , Rice Univ. , Houston (1963)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Lohwater, "The boundary behaviour of analytic functions" ''Itogi Nauk. Mat. Anal.'' , '''10''' (1973) pp. 99–259 (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> W. Rudin, "Function theory in polydiscs" , Benjamin (1969)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> G.M. Khenkin, E.M. Chirka, "Boundary properties of holomorphic functions of several complex variables" ''J. Soviet Math.'' , '''5''' : 5 (1971) pp. 612–687 ''Itogi Nauk. i Tekhn. Sovrem. Probl. Mat.'' , '''4''' (1975) pp. 13–142</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.V. Golubev, "Univalent analytic functions. Automorphic functions" , Moscow (1961) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> S.Ya. Khavinson, "Analytic functions of bounded type" ''Itogi Nauk. Mat. Anal. 1963'' (1965) pp. 5–80 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Noshiro, "Cluster sets" , Springer (1960)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.R. MacLane, "Asymptotic values of holomorphic functions" , ''Rice Univ. Studies, Math. Monographs'' , '''49''' : 1 , Rice Univ. , Houston (1963)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Lohwater, "The boundary behaviour of analytic functions" ''Itogi Nauk. Mat. Anal.'' , '''10''' (1973) pp. 99–259 (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> W. Rudin, "Function theory in polydiscs" , Benjamin (1969)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> G.M. Khenkin, E.M. Chirka, "Boundary properties of holomorphic functions of several complex variables" ''J. Soviet Math.'' , '''5''' : 5 (1971) pp. 612–687 ''Itogi Nauk. i Tekhn. Sovrem. Probl. Mat.'' , '''4''' (1975) pp. 13–142</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Sokhotskii's theorem is better known as the Casorati–Weierstrass theorem. In (4) the first integral on the right-hand side is called the outer factor, while the other factors on the right-hand side form together the inner factor; the latter has absolute boundary values 1 almost-everywhere. If the outer factor in (4) equals 1, | + | Sokhotskii's theorem is better known as the Casorati–Weierstrass theorem. In (4) the first integral on the right-hand side is called the outer factor, while the other factors on the right-hand side form together the inner factor; the latter has absolute boundary values 1 almost-everywhere. If the outer factor in (4) equals 1, $ f $ |
| + | is called an inner function. Recent general references are [[#References|[a2]]], [[#References|[a3]]]. | ||
| − | For smooth domains | + | For smooth domains $ \Omega $ |
| + | in $ \mathbf C ^ {n} $, | ||
| + | $ n \geq 2 $, | ||
| + | there is a strong version of Fatou's theorem for $ H ^ {p} ( \Omega ) $ | ||
| + | and $ N ^ {*} ( \Omega ) $: | ||
| + | Boundary values exist almost-everywhere (or even better than almost-everywhere) if the boundary is approached over admissible approach regions, see [[#References|[a5]]], [[#References|[a7]]]. In contrast with the one-dimensional case, zero sets of $ H ^ {p} $- | ||
| + | functions can be essentially different for different values of $ p $, | ||
| + | see [[#References|[11]]], [[#References|[a5]]]. A characterization of zero sets of functions of Nevanlinna class on smooth strongly pseudo-convex domains was obtained by G.M. Khenkin and, independently, by H. Skoda, see [[#References|[a5]]]. A.B. Aleksandrov and E. Løw proved independently the existence of non-constant inner functions for the unit-ball in $ \mathbf C ^ {n} $, | ||
| + | see [[#References|[a1]]], [[#References|[a4]]]. In an other direction, $ H ^ {p} $- | ||
| + | spaces have been introduced for the upper half-space in $ \mathbf R ^ {n} $, | ||
| + | [[#References|[a6]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.B. Aleksandrov, "The existence of inner functions in the ball" ''Math. USSR Sb.'' , '''46''' (1983) pp. 143–159</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-B. Garnett, "Bounded analytic functions" , Acad. Press (1981)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P. Koosis, "Introduction to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017330/b017330266.png" />-spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Løw, "A construction of inner functions on the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017330/b017330267.png" />" ''Invent. Math.'' , '''67''' (1982) pp. 223–229</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017330/b017330268.png" />" , Springer (1980)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970) pp. Chapt. 7</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E.M. Stein, "Boundary behavior of holomorphic functions of several complex variables" , Princeton Univ. Press (1972)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.B. Aleksandrov, "The existence of inner functions in the ball" ''Math. USSR Sb.'' , '''46''' (1983) pp. 143–159</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.-B. Garnett, "Bounded analytic functions" , Acad. Press (1981)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P. Koosis, "Introduction to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017330/b017330266.png" />-spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Løw, "A construction of inner functions on the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017330/b017330267.png" />" ''Invent. Math.'' , '''67''' (1982) pp. 223–229</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017330/b017330268.png" />" , Springer (1980)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970) pp. Chapt. 7</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> E.M. Stein, "Boundary behavior of holomorphic functions of several complex variables" , Princeton Univ. Press (1972)</TD></TR></table> | ||
Revision as of 06:29, 30 May 2020
Properties of analytic functions that are displayed as the function approaches the boundary of its domain of definition.
It can be said that the study of boundary properties of analytic functions, understood in the widest sense of the word, began with the Sokhotskii theorem and the Picard theorem about the behaviour of analytic functions in a neighbourhood of isolated essential singular points (cf. Essential singular point), which were obtained in the second half of the 19th century. The terms relevant to this approach to the study of boundary properties of analytic functions — which is now called the theory of prime ends and cluster sets (cf. Limit elements) — first appeared in a course given by P. Painlevé in 1895. The dissertation of P. Fatou (1906) is the first systematic study of certain boundary properties of analytic functions in a neighbourhood of the continuous boundary of their domain of definition. The theory of boundary properties made considerable advances in the first third of the 20th century, owing to the work of several scientists; it resumed its rapid advance in the second half of that century, accompanied by the appearance of new ideas and methods, novel directions and objects of study. Its development is closely connected with various fields of mathematical analysis and mathematics in general, first and foremost with probability theory, the theory of harmonic functions, the theory of conformal mapping, boundary value problems of analytic function theory, potential theory, value-distribution theory, Riemann surfaces, subharmonic functions and function algebras. The theory of boundary properties of analytic functions is closely connected with various fields of application of mathematics by way of boundary value problems.
Since the study of boundary properties is connected, in the first place, with the geometry of the boundary $ \Gamma $ of the domain of definition $ D $ of an analytic function $ f(z) $ in one complex variable $ z $, three main approaches can be distinguished in the theory of boundary properties of analytic functions.
a) The study of the behaviour of $ f(z) $ in a neighbourhood of an isolated boundary point $ a \in \Gamma $. The most important case is that of an essential singular point $ a $, which is dealt with in the theorems of Sokhotskii, Picard, Julia, and Iversen (cf. Sokhotskii theorem; Picard theorem; Julia theorem; Iversen theorem).
b) The study of the behaviour of $ f(z) $ in the case when the boundary $ \Gamma $ is an everywhere-discontinuous set. V.V. Golubev's dissertation Single-valued analytic functions with a perfect set of singular points (1916, cf. [1]) was of great importance in this connection.
c) The study of the behaviour of $ f(z) $ when the domain $ D $ is bounded by a continuous closed curve $ \Gamma $ and, in particular, by the unit circle.
Cases a) and c) are, in a sense, extreme cases, while case b) is intermediate. Case c), which is discussed below, has been the subject of most intense study.
Let an analytic function $ f(z) $ be defined in a finite simply-connected domain $ D $ of the complex $ z $- plane bounded by a rectifiable Jordan curve $ \Gamma $. The following problems are fundamental in the classical approach to the study of boundary properties of analytic functions.
1) The problem of the existence of boundary values, i.e. the question under which conditions and in which sense the boundary values of $ f(z) $ exist as the point $ z $ approaches $ \Gamma $. This problem, as well as the succeeding ones, can be formulated in a different manner as the problem of identifying sufficiently extensive classes of analytic functions in $ D $ that have, in some sense, boundary values for sufficiently large sets of points on $ \Gamma $.
2) The problem of boundary representation of $ f(z) $, i.e. the problem under which conditions and with what kind of analytic apparatus the dependence of $ f(z) $ on its boundary values on $ \Gamma $ can be expressed. Clearly, this apparatus will be different for different classes of analytic functions.
3) The uniqueness problem, or the problem of the properties that a set $ E \subset \Gamma $ should have such that two analytic functions of a given class coincide in $ D $ if their boundary values on $ E $ are identical.
The first result in the solution of the existence problem is the theorem of Fatou (1906): If an analytic function is bounded in the unit disc $ D = \{ {z } : {| z | < 1 } \} $, $ | f(z) | \leq M $, then radial boundary, or limit, values $ f(e ^ {i \theta } ) = \lim\limits _ {r \rightarrow 1 - 0 } f (re ^ {i \theta } ) $ exist almost everywhere with respect to the Lebesgue measure on the unit circle $ \Gamma = \{ {z } : {| z | = 1 } \} $. It can be shown that, under these conditions, not only radial, but also angular boundary values, or boundary values along all non-tangential paths, exist almost everywhere on $ \Gamma $. This means that, for almost-all points $ e ^ {i \theta } \in \Gamma $, $ f(z) $ tends to a definite limit $ f ( e ^ {i \theta } ) $ as $ z $ tends to the point $ e ^ {i \theta } $ while remaining within an arbitrary fixed angle
$$ \Delta (e ^ {i \theta } , \epsilon ) = \ \{ | z | < 1 \} \cap \left \{ | \mathop{\rm arg} (e ^ {i \theta } - z) | < { \frac \pi {2} } - \epsilon \right \} , $$
$ \epsilon > 0 $, of width $ \pi - 2 \epsilon < \pi $, with apex at the point $ e ^ {i \theta } $, bisected by the radius drawn through the point $ e ^ {i \theta } $. Fatou's theorem cannot, in a certain sense, be improved upon; it was in fact shown by N.N. Luzin (1919) that for any set $ E \subset \Gamma $ of measure zero on $ \Gamma $ there exists a bounded analytic function $ f(z) $ not having radial limits on $ E $.
The class of bounded analytic functions in a domain $ D $ is denoted by $ B(D) $ or $ H ^ \infty (D) $. Following the results of Fatou, the next problem appeared to be the generalization of his theorems to wider classes of functions. One distinguishes between the following basic classes of functions in the unit disc $ D $, which are related by proper inclusions:
$$ \tag{1 } A (D) \subset B (D) = H ^ \infty (D) \subset \ H ^ {p} (D) \subset N ^ {*} (D) \subset N (D). $$
The class $ A(D) $ is the class of single-valued analytic functions in $ D $ that are continuous in the closed domain $ D \cup \Gamma = \overline{D}\; $.
The classes $ H ^ {p} (D) $, for all positive numbers $ p $, are defined by the condition
$$ \tag{2 } \| f \| _ {p} = \ \sup _ {0 < r < 1 } \ \left \{ \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } | f (re ^ {i \phi } ) | ^ {p} \ d \phi \right \} ^ {1/p} = \ C (f, p) < $$
$$ < \ + \infty . $$
The proper inclusions $ H ^ \infty \subset H ^ {p _ {1} } \subset H ^ {p _ {2} } $ are valid for any $ 0 < p _ {1} < p _ {2} < + \infty $. The classes $ H ^ {p} $ were first introduced by G.H. Hardy (1915), and are often named Hardy classes. If $ 1 \leq p < \infty $, one can introduce the norm (2) on $ H ^ {p} $, and the norm
$$ \| f \| _ \infty = \ \| f \| _ {B} = \ \sup _ {z \in D } \ | f(z) | $$
on $ H ^ \infty $; the classes $ H ^ {p} $, $ 1 \leq p \leq + \infty $, have a natural structure of a vector space, and become Banach Hardy spaces. If $ 0 < p < 1 $, it is only possible to introduce the metric $ \rho _ {p} (f, g) = \| f - g \| _ {p} ^ {p} $ on $ H ^ {p} $, which converts the latter into a complete metric non-normable space. The class of bounded analytic functions $ B = H ^ \infty $ is contained in any class $ H ^ {p} $, $ p > 0 $.
The class $ N(D) $ of certain meromorphic functions $ f(z) $ in the unit disc $ D $ is said to be the class of functions of bounded characteristic; it was introduced in 1924 by R. Nevanlinna. The class $ N(D) $ can be characterized as the set of meromorphic functions $ f(z) $ in $ D $ that can be represented as the ratio of two bounded regular functions $ f _ {1} (z) $ and $ f _ {2} (z) $ in $ D $, $ f(z) = f _ {1} (z)/f _ {2} (z) $.
All regular functions $ f(z) \in N(D) $ form a subclass $ N ^ {*} (D) $, and $ f(z) \in N ^ {*} (D) $ if and only if the condition
$$ \tag{3 } \sup _ {0 < r < 1 } \ \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } \mathop{\rm ln} ^ {+} | f (re ^ {i \phi } ) | \ d \phi = C (f) < + \infty , $$
where $ \mathop{\rm ln} ^ {+} x = \mathop{\rm ln} x $ if $ \mathop{\rm ln} x \geq 0 $ and $ \mathop{\rm ln} ^ {+} x = 0 $ if $ \mathop{\rm ln} x < 0 $, is fulfilled. The class $ N ^ {*} (D) $ contains all classes $ H ^ {p} $, $ 0 < p \leq + \infty $.
The classes $ H ^ {p} $ have the following generalization. Let $ \psi (t) $ be a strictly-convex function for $ - \infty < t < + \infty $, i.e. a non-negative, convex, non-decreasing function such that $ \psi (t) / t \rightarrow + \infty $ as $ t \rightarrow + \infty $. The class $ H _ \psi (D) $ is then defined by the condition
$$ \tag{2'} \sup _ {0 < r < 1 } \ \psi ^ {-1} \left \{ \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } \psi ( \mathop{\rm ln} | f (re ^ {i \phi } ) | ) d \phi \right \} = \ C (f, \psi ) < $$
$$ < \ + \infty , $$
compare with condition (2), where $ \psi (t) = e ^ {pt} $.
The principal result obtained for the problem of the existence of boundary values in the case of the unit disc $ D $ states that each meromorphic function $ f (z) $ of bounded characteristic in $ D $ has angular boundary values $ f (e ^ {i \theta } ) $ almost everywhere on $ \Gamma $; these boundary values are such that the function $ \mathop{\rm ln} | f ( e ^ {i \theta } ) | $ is Lebesgue integrable on $ \Gamma $. The following additional property is displayed by the classes $ H ^ {p} $, $ 0 < p < + \infty $, or $ H _ \psi $: The function $ | f (e ^ {i \theta } ) | ^ {p} $ or, correspondingly, $ \psi ( \mathop{\rm ln} | f ( e ^ {i \theta } ) | ) ^ {p} $ is Lebesgue integrable on $ \Gamma $. For bounded functions $ f(z) $, $ | f(z) | \leq M $, one has instead of the above, $ \mathop{\rm esssup} | f (e ^ {i \theta } ) | \leq M $, $ 0 \leq \theta \leq 2 \pi $. Thus, condition (3) is the widest sufficient condition on the average increase of an analytic function $ f(z) $, as $ | z | \rightarrow 1 $, that ensures the existence of angular boundary values almost everywhere on $ \Gamma $.
It has been shown that condition (3) cannot be substantially weakened. Thus, it was shown by A. Zygmund that for an arbitrary increasing function $ \psi (t) $, $ \psi (t) / t \rightarrow 0 $ as $ 0 < t \uparrow + \infty $, there exists an analytic function $ f(z) $ in $ D $ such that
$$ \sup _ {0 < r < 1 } \ \int\limits _ { 0 } ^ { {2 } \pi } \psi ( \mathop{\rm ln} ^ {+} | f (re ^ {i \phi } ) | ) \ d \phi < + \infty , $$
but which has no boundary values anywhere on $ \Gamma $. Even if the maximum $ M (r; f) = \max \{ {| f(z) | } : {| z | = r } \} $ grows as slowly as one pleases, there still exist analytic functions without radial boundary values.
The boundary representation of functions $ f(z) $ of class $ N(D) $, characterizing the functions of this class, has the form
$$ \tag{4 } f (z) = z ^ {m} e ^ {i \lambda } \frac{B _ {1} (z; a _ \mu ) }{B _ {2} (z; b _ \nu ) } \times $$
$$ \times \mathop{\rm exp} \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } \mathop{\rm ln} | f (e ^ {i \theta } ) | \frac{e ^ {i \theta } + z }{e ^ {i \theta } - z } d \theta \times $$
$$ \times \mathop{\rm exp} \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } \frac{e ^ {i \theta } + z }{e ^ {i \theta } - z } d \Phi ( \theta ), $$
where $ m $ is an integer, $ m = k $ if the point $ z = 0 $ is a zero of multiplicity $ k $ and $ m = - k $ if $ z = 0 $ is a pole of multiplicity $ k $; $ \lambda $ is a real number;
$$ \tag{5 } B _ {1} (z; a _ \mu ) = \ \prod _ {\mu = 1 } ^ \infty \frac{| a _ \mu | }{a _ \mu } \frac{a _ \mu - z }{1 - \overline{ {a _ \mu }}\; z } $$
is the Blaschke product taken over all the zeros $ a _ \mu \neq 0 $ of $ f (z) $ inside $ D $ taking into account their multiplicity; $ B _ {2} (z; b _ \nu ) $ is the Blaschke product of type (5) taken over all poles $ b _ \nu \neq 0 $ of $ f(z) $ in $ D $; and $ \Phi ( \theta ) $ is a singular function of bounded variation on $ [0, 2 \pi ] $ with a derivative that vanishes almost everywhere. In (4), the last integral is of Lebesgue–Stieltjes type, while the first is of Lebesgue type.
It was shown by M.M. Dzhrbashyan [10] that the theory of meromorphic functions of bounded characteristic can be considerably extended. It is possible, in fact, to introduce a family of classes of meromorphic functions $ N _ \alpha $ depending on a continuous parameter $ \alpha $, $ -1 < \alpha < + \infty $, and the classes $ N _ \alpha $ are characterized by representations yielding (4) when $ \alpha = 0 $. As $ \alpha $ increases, the classes $ N _ \alpha $ become larger, and $ N _ {0} $ becomes identical with Nevanlinna's class $ N $.
For analytic functions $ f(z) \in N ^ {*} (D) $ in the representation (4) one must put $ B _ {2} (z; b _ \nu ) \equiv 1 $. For the functions $ f(z) \in H ^ {p} $, $ 0 < p \leq + \infty $, or $ \in H _ \psi $, in the representation (4) one has $ B _ {2} (z; b _ \nu ) \equiv 1 $, and $ \Phi ( \theta ) $ is a non-increasing function of the indicated type. See also Cauchy integral.
The first results in the uniqueness problem were obtained in 1916 by the brothers F. and M. Riesz: If a function $ f(z) \in H ^ \infty $ has radial boundary values $ f (e ^ {i \theta } ) = 0 $ on a set $ E \subset \Gamma $ of positive Lebesgue measure on $ \Gamma $, then $ f(z) \equiv 0 $ in $ D $. The representation (4) makes it possible to extend this theorem to meromorphic functions of bounded characteristic (cf. Function of bounded form). N.N. Luzin (1919) constructed, for any set $ E \subset \Gamma $ of measure zero, an analytic function $ f(z) $ such that $ f ( e ^ {i \theta } ) = 0 $ everywhere on $ E $ as $ z \rightarrow e ^ {i \theta } $ in an arbitrary manner, but $ f (z) $ is not identically equal to zero. The deepest and most general boundary uniqueness theorems for meromorphic functions of general form were obtained in 1925 by Luzin and I.I. Privalov (cf. Uniqueness properties of analytic functions; Luzin–Privalov theorems).
Consider the case of an arbitrary plane domain $ D $; for the sake of brevity, only simply-connected domains $ D $ with a rectifiable boundary $ \Gamma $ will be discussed. The conditions (2), (3) and (2'}) are equivalent to stipulating that the subharmonic functions $ {| f(z) | } ^ {p} $, $ \mathop{\rm ln} ^ {+} | f(z) | $ and $ \psi ( \mathop{\rm ln} | f (z) | ) $, respectively, have a harmonic majorant in $ D $. In such a form these conditions are fully suitable, and furnish a natural definition of the classes $ H ^ {p} $, $ N ^ {*} $ and $ H _ \psi $ in arbitrary domains. It is known that a rectifiable curve $ \Gamma $ has a definite tangent and normal at almost all of its points. The inclusions (1) remain valid, as does Fatou's theorem on the almost-everywhere existence on $ \Gamma $ of angular boundary values for the class $ N ^ {*} $. Here, as the bisectrix of the angular domains $ \Delta ( \zeta , \epsilon ) $ the normal to $ \Gamma $ at the point $ \zeta \in \Gamma $ is taken. The Riesz uniqueness theorem for the class $ N ^ {*} $ is also applicable.
V.I. Smirnov also introduced the frequently employed classes $ E ^ {p} $, $ p > 0 $, for the case of an arbitrary domain $ D $. These classes have the following definition: $ f(z) \in E ^ {p} (D) $ if there exist a sequence of contours $ \{ \Gamma _ {j} \} \subset D $, $ \Gamma _ {j} \rightarrow \Gamma $, such that
$$ \sup _ {\{ \Gamma _ {j} \} } \ \int\limits _ {\Gamma _ {j} } | f (z) | ^ {p} | dz | = C (f, p) < + \infty . $$
The classes $ E ^ {p} $ are especially convenient in the study of problems of representation of functions in the form of a Cauchy integral.
Of major interest is the study of the boundary properties of analytic functions realizing a conformal mapping. Let a function $ z = F (w) $ realize a conformal mapping of the unit disc $ | w | < 1 $ onto a domain $ D $ of the $ z $- plane with a rectifiable boundary $ \Gamma $. It has been shown, for example, that in such a case the derivative $ F ^ { \prime } (w) $ belongs to the Hardy class $ H ^ {1} $ in the disc $ | w | < 1 $, so that it is representable in the form (4) with $ B _ {2} \equiv 1 $ and a non-increasing singular function $ \Phi ( \theta ) $. Smirnov pointed out the importance of the class $ S $ of such domains $ D $ for which this singular function $ \Phi ( \theta ) \equiv 0 $. In 1937 M.V. Keldysh and M.A. Lavrent'ev constructed an example of a domain with a rectifiable boundary that is not included in the Smirnov classes just mentioned; this renders the characterization of domains of Smirnov type even more important.
Numerous workers also attempt to study boundary properties of analytic functions $ f(z) $ in several variables $ z = (z _ {1} \dots z _ {n} ) $. Let $ D = U ^ {n} = \{ {z \in \mathbf C ^ {n} } : {| z _ {j} | < 1, j = 1 \dots n } \} $ be the unit polydisc, and let $ T ^ {n} = \{ {z \in \mathbf C ^ {n} } : {| z _ {j} | = 1, j = 1 \dots n } \} $ be its skeleton. The class $ N ^ {*} (D) $ of analytic functions $ f(z) $ in $ D $ is defined by the condition
$$ \sup _ {0 < r < 1 } \ \int\limits _ {T ^ {n} } \mathop{\rm ln} ^ {+} | f(rz) | \ dm _ {n} (z) = \ C (f) < + \infty , $$
which is analogous to (3), while the classes $ H ^ {p} (D) $ or $ H _ \psi (D) $ by the condition of the type ( $ \psi (t) = e ^ {pt} $ for the case $ H ^ {p} (D) $, $ p > 0 $):
$$ \sup _ {0 < r < 1 } \ \psi ^ {-1} \left \{ \int\limits _ {T ^ {n} } \psi ( \mathop{\rm ln} | f (rz) |) \ dm _ {n} (z) \right \} = \ C(f, \psi ) < + \infty , $$
where $ m _ {n} $ is the normalized Haar measure on $ T ^ {n} $, $ m _ {n} (T ^ {n} ) = 1 $. Inclusions of the type $ B = H ^ \infty \subset H _ \psi \subset N ^ {*} $ are preserved. Analytic functions $ f(z) \in N ^ {*} (D) $ have "radial" boundary values $ f ^ {*} (z) = \lim\limits _ {r \rightarrow 1 - 0 } f(rz) $, $ z \in T ^ {n} $, almost everywhere on $ T ^ {n} $ with respect to the Haar measure $ m _ {n} $; and $ \mathop{\rm ln} ^ {+} | f ^ {*} (z) | $ is summable on $ T _ {n} $ with respect to $ m _ {n} $. Sufficiently simple and general characteristics for boundary representations and uniqueness properties of functions $ f(z) $ in $ U ^ {n} $ for $ n > 1 $ have not yet (1986) been found.
Many boundary properties may be applied to various generalizations of analytic functions, in particular to abstract analytic functions $ f: D \rightarrow X $, which have values in, say, a separable locally convex topological space $ X $ over the field $ \mathbf C $.
References
| [1] | V.V. Golubev, "Univalent analytic functions. Automorphic functions" , Moscow (1961) (In Russian) |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [4] | S.Ya. Khavinson, "Analytic functions of bounded type" Itogi Nauk. Mat. Anal. 1963 (1965) pp. 5–80 (In Russian) |
| [5] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [6] | K. Noshiro, "Cluster sets" , Springer (1960) |
| [7] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 9 |
| [8] | G.R. MacLane, "Asymptotic values of holomorphic functions" , Rice Univ. Studies, Math. Monographs , 49 : 1 , Rice Univ. , Houston (1963) |
| [9] | A. Lohwater, "The boundary behaviour of analytic functions" Itogi Nauk. Mat. Anal. , 10 (1973) pp. 99–259 (In Russian) |
| [10] | M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian) |
| [11] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
| [12] | G.M. Khenkin, E.M. Chirka, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 : 5 (1971) pp. 612–687 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 4 (1975) pp. 13–142 |
Comments
Sokhotskii's theorem is better known as the Casorati–Weierstrass theorem. In (4) the first integral on the right-hand side is called the outer factor, while the other factors on the right-hand side form together the inner factor; the latter has absolute boundary values 1 almost-everywhere. If the outer factor in (4) equals 1, $ f $ is called an inner function. Recent general references are [a2], [a3].
For smooth domains $ \Omega $ in $ \mathbf C ^ {n} $, $ n \geq 2 $, there is a strong version of Fatou's theorem for $ H ^ {p} ( \Omega ) $ and $ N ^ {*} ( \Omega ) $: Boundary values exist almost-everywhere (or even better than almost-everywhere) if the boundary is approached over admissible approach regions, see [a5], [a7]. In contrast with the one-dimensional case, zero sets of $ H ^ {p} $- functions can be essentially different for different values of $ p $, see [11], [a5]. A characterization of zero sets of functions of Nevanlinna class on smooth strongly pseudo-convex domains was obtained by G.M. Khenkin and, independently, by H. Skoda, see [a5]. A.B. Aleksandrov and E. Løw proved independently the existence of non-constant inner functions for the unit-ball in $ \mathbf C ^ {n} $, see [a1], [a4]. In an other direction, $ H ^ {p} $- spaces have been introduced for the upper half-space in $ \mathbf R ^ {n} $, [a6].
References
| [a1] | A.B. Aleksandrov, "The existence of inner functions in the ball" Math. USSR Sb. , 46 (1983) pp. 143–159 |
| [a2] | J.-B. Garnett, "Bounded analytic functions" , Acad. Press (1981) |
| [a3] | P. Koosis, "Introduction to 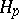 -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) -spaces. With an appendix on Wolff's proof of the corona theorem" , Cambridge Univ. Press (1980) |
| [a4] | E. Løw, "A construction of inner functions on the unit ball in  " Invent. Math. , 67 (1982) pp. 223–229 " Invent. Math. , 67 (1982) pp. 223–229 |
| [a5] | W. Rudin, "Function theory in the unit ball in 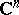 " , Springer (1980) " , Springer (1980) |
| [a6] | E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970) pp. Chapt. 7 |
| [a7] | E.M. Stein, "Boundary behavior of holomorphic functions of several complex variables" , Princeton Univ. Press (1972) |
Boundary properties of analytic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_properties_of_analytic_functions&oldid=46130