Bound variable
bound occurrence of a variable
A type of occurrence of a variable in a linguistic expression. An exact definition for each formalized language depends on the rules of formation of the language. It is not possible to substitute objects in place of a bound variable, since such a substitution would lead to meaningless expressions. But the replacement of a bound variable, where it occurs, by a new (for a given expression) variable leads to an expression with the same meaning. For example, in the expressions
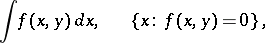 |
 is a bound variable. Replacing
is a bound variable. Replacing  by a number leads to a meaningless expression, whereas by writing
by a number leads to a meaningless expression, whereas by writing  everywhere instead of
everywhere instead of  one obtains an expression with exactly the same meaning.
one obtains an expression with exactly the same meaning.
Bound variables always arise in applying to an expression  with free occurrences of a variable
with free occurrences of a variable  an operator variable
an operator variable  (see Free variable). In the resulting expression, all the occurrences of
(see Free variable). In the resulting expression, all the occurrences of  in
in  that were previously free become bound. We mention below certain operators that are often used (next to the operators
that were previously free become bound. We mention below certain operators that are often used (next to the operators 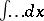 and
and 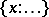 ), in which
), in which  is an operator variable:
is an operator variable:
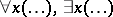 , that is, the universal and existential quantifiers;
, that is, the universal and existential quantifiers;
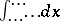 , that is, a definite integral with respect to
, that is, a definite integral with respect to  ;
;
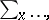 that is, summation over
that is, summation over  ;
;
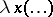 , that is, a function of
, that is, a function of  the value of which at
the value of which at  is
is 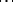 . Specific linguistic expressions can be substituted in place of the dots.
. Specific linguistic expressions can be substituted in place of the dots.
In real (non-formalized) mathematical texts it is possible to have a non-unique use for one and the same expression; in this connection distinguishing a bound variable in a given expression depends on the context and meaning of the expression. In formalized languages there is a formal procedure for distinguishing free and bound occurrences of variables.
Bound variable. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bound_variable&oldid=14900