Bott periodicity theorem
A fundamental theorem in 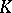 -theory which, in its simplest form, states that for any (compact) space
-theory which, in its simplest form, states that for any (compact) space 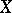 there exists an isomorphism between the rings
there exists an isomorphism between the rings 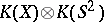 and
and 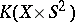 . More generally, if
. More generally, if 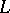 is a complex vector bundle over
is a complex vector bundle over 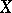 and
and 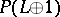 is the projectivization of
is the projectivization of 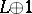 , then the ring
, then the ring 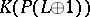 is a
is a 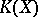 -algebra with one generator
-algebra with one generator 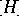 and a unique relation
and a unique relation 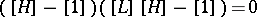 , where
, where 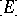 is the image of a vector bundle
is the image of a vector bundle 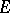 in
in 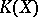 and
and 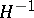 is the Hopf fibration over
is the Hopf fibration over 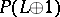 . This fact is equivalent to the existence of a Thom isomorphism in
. This fact is equivalent to the existence of a Thom isomorphism in 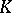 -theory for complex vector bundles. In particular,
-theory for complex vector bundles. In particular, 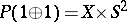 . Bott's periodicity theorem was first demonstrated by R. Bott [1] using Morse theory, and was then re-formulated in terms of
. Bott's periodicity theorem was first demonstrated by R. Bott [1] using Morse theory, and was then re-formulated in terms of 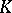 -theory [6]; an analogous theorem has also been demonstrated for real fibre bundles.
-theory [6]; an analogous theorem has also been demonstrated for real fibre bundles.
Bott's periodicity theorem establishes the property of the stable homotopy type of the unitary group 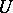 , consisting in the fact that
, consisting in the fact that 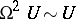 , where
, where 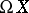 is the space of loops on
is the space of loops on 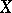 , and
, and 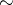 is weak homotopy equivalence, in particular
is weak homotopy equivalence, in particular 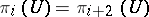 for
for 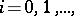 where
where 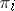 is the
is the 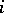 -th homotopy group. Similarly, for the orthogonal group
-th homotopy group. Similarly, for the orthogonal group 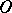 :
:
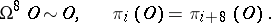 |
References
| [1] | R. Bott, "The stable homotopy of the classical groups" Ann. of Math. (2) , 70 : 2 (1959) pp. 313–337 |
| [2] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) |
| [3] | M.F. Atiyah, " -theory: lectures" , Benjamin (1967) -theory: lectures" , Benjamin (1967) |
| [4] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [5] | J.C. Moore, "On the periodicity theorem for complex vector bundles" , Sem. H. Cartan (1959–1960) |
| [6] | M.F. Atiyah, R. Bott, "On the periodicity theorem for complex vector bundles" Acta Math. , 112 (1964) pp. 229–247 |
Comments
References
| [a1] | R. Bott, "Lectures on 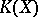 " , Benjamin (1969) " , Benjamin (1969) |
| [a2] | M. Karoubi, " -theory" , Springer (1978) -theory" , Springer (1978) |
Bott periodicity theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bott_periodicity_theorem&oldid=18004