Borsuk problem
One of the fundamental problems in combinatorial geometry: Is it possible, for any bounded set of diameter 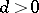 in an
in an  -dimensional Euclidean space, to make a decomposition into not more than
-dimensional Euclidean space, to make a decomposition into not more than  subsets with diameters smaller than
subsets with diameters smaller than 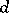 ? The problem was formulated by K. Borsuk [1] who noted that it was not possible to subdivide an
? The problem was formulated by K. Borsuk [1] who noted that it was not possible to subdivide an  -dimensional simplex and an
-dimensional simplex and an  -dimensional sphere in
-dimensional sphere in 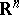 into
into  parts of a smaller diameter. The problem has a positive solution for
parts of a smaller diameter. The problem has a positive solution for 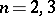 , but only partial results have been obtained for
, but only partial results have been obtained for  . Thus, for instance, the problem has been positively solved for any bounded smooth convex set in
. Thus, for instance, the problem has been positively solved for any bounded smooth convex set in 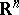 [2]. It has been proved that the solution of Borsuk's problem can be reduced to the case of sets of constant width. If
[2]. It has been proved that the solution of Borsuk's problem can be reduced to the case of sets of constant width. If 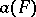 is the smallest number of parts of a diameter smaller than
is the smallest number of parts of a diameter smaller than 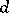 into which a set
into which a set 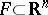 can be subdivided, then the equality
can be subdivided, then the equality 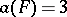 is valid for a figure
is valid for a figure 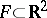 of diameter
of diameter 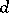 if and only if
if and only if 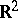 contains a unique figure of constant width
contains a unique figure of constant width 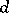 containing
containing 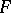 [3]. This fact cannot be directly generalized to the case
[3]. This fact cannot be directly generalized to the case 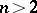 . The Borsuk problem is closely related to the illumination problem and to the Hadwiger hypothesis, which is a generalization of the Borsuk problem in which
. The Borsuk problem is closely related to the illumination problem and to the Hadwiger hypothesis, which is a generalization of the Borsuk problem in which 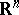 is replaced by a finite-dimensional normed space.
is replaced by a finite-dimensional normed space.
References
| [1] | K. Borsuk, "Drei Sätze über die  -dimensionale euklidische Sphäre" Fund. Math. , 20 (1933) pp. 177–190 -dimensionale euklidische Sphäre" Fund. Math. , 20 (1933) pp. 177–190 |
| [2] | B. Grünbaum, "Borsuk's problem and related questions" V.L. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 271–284 |
| [3] | V.G. Boltyanskii, "On decomposition of plane figures in parts of least diameter" Colloq. Math. , 21 : 2 (1967) pp. 253–263 (In Russian) |
Comments
References
| [a1] | V.G. Boltyanskii, I.Ts. Gokhberg, "Sätze und Probleme der Kombinatorische Geometrie" , Deutsch. Verlag Wissenschaft. (1972) (Translated from Russian) |
Borsuk problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borsuk_problem&oldid=31851