Borsuk-Ulam theorem
In the Borsuk–Ulam theorem (K. Borsuk, 1933 [a2]), topological and symmetry properties are used for coincidence assertions for mappings defined on the  -dimensional unit sphere
-dimensional unit sphere  . Obviously, the following three versions of this result are equivalent:
. Obviously, the following three versions of this result are equivalent:
1) For every continuous mapping  , there exists an
, there exists an  with
with  .
.
2) For every odd continuous mapping  , there exists an
, there exists an  with
with  .
.
3) If there exists an odd continuous mapping  , then
, then  . The Borsuk–Ulam theorem is equivalent, among others, to the fact that odd continuous mappings
. The Borsuk–Ulam theorem is equivalent, among others, to the fact that odd continuous mappings  are essential (cf. Antipodes), to the Lyusternik–Shnirel'man–Borsuk covering theorem and to the Krein–Krasnosel'skii–Mil'man theorem on the existence of vectors "orthogonal" to a given linear subspace [a3].
are essential (cf. Antipodes), to the Lyusternik–Shnirel'man–Borsuk covering theorem and to the Krein–Krasnosel'skii–Mil'man theorem on the existence of vectors "orthogonal" to a given linear subspace [a3].
The Borsuk–Ulam theorem remains true:
a) if one replaces 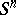 by the boundary
by the boundary 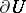 of a bounded neighbourhood
of a bounded neighbourhood  of
of  with
with  ;
;
b) for continuous mappings 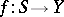 , where
, where  is the unit sphere in a Banach space
is the unit sphere in a Banach space  ,
,  ,
,  , a linear subspace of
, a linear subspace of 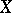 and
and  a compact mapping (for versions 1) and 2)).
a compact mapping (for versions 1) and 2)).
For more general symmetries, the following extension of version 3) holds:
Let  and
and 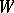 be finite-dimensional orthogonal representations of a compact Lie group
be finite-dimensional orthogonal representations of a compact Lie group 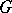 , such that for some prime number
, such that for some prime number 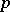 , some subgroup
, some subgroup  acts freely on the unit sphere
acts freely on the unit sphere  . If there exists a
. If there exists a  -mapping
-mapping  , then
, then 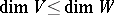 .
.
For related results under weaker conditions, cf. [a1]; for applications, cf. [a4].
References
| [a1] | T. Bartsch, "On the existence of Borsuk–Ulam theorems" Topology , 31 (1992) pp. 533–543 |
| [a2] | K. Borsuk, "Drei Sätze über die  -dimensionale Sphäre" Fund. Math. , 20 (1933) pp. 177–190 -dimensionale Sphäre" Fund. Math. , 20 (1933) pp. 177–190 |
| [a3] | M.G. Krein, M.A. Krasnosel'skii, D.P. Mil'man, "On the defect numbers of linear operators in a Banach space and some geometrical questions" Sb. Trud. Inst. Mat. Akad. Nauk Ukrain. SSR , 11 (1948) pp. 97–112 (In Russian) |
| [a4] | H. Steinlein, "Borsuk's antipodal theorem and its generalizations and applications: a survey. Méthodes topologiques en analyse non linéaire" , Sém. Math. Supér. Montréal, Sém. Sci. OTAN (NATO Adv. Study Inst.) , 95 (1985) pp. 166–235 |
Borsuk-Ulam theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borsuk-Ulam_theorem&oldid=16557