Borel fixed-point theorem
A connected solvable algebraic group 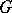 acting regularly (cf. Algebraic group of transformations) on a non-empty complete algebraic variety
acting regularly (cf. Algebraic group of transformations) on a non-empty complete algebraic variety 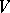 over an algebraically-closed field
over an algebraically-closed field 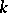 has a fixed point in
has a fixed point in 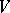 . It follows from this theorem that Borel subgroups (cf. Borel subgroup) of algebraic groups are conjugate (The Borel–Morozov theorem). The theorem was demonstrated by A. Borel [1]. Borel's theorem can be generalized to an arbitrary (not necessarily algebraically-closed) field
. It follows from this theorem that Borel subgroups (cf. Borel subgroup) of algebraic groups are conjugate (The Borel–Morozov theorem). The theorem was demonstrated by A. Borel [1]. Borel's theorem can be generalized to an arbitrary (not necessarily algebraically-closed) field 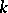 : Let
: Let 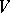 be a complete variety defined over a field
be a complete variety defined over a field 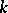 on which a connected solvable
on which a connected solvable 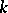 -split group
-split group 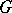 acts regularly, then the set of rational
acts regularly, then the set of rational 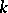 -points
-points 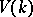 is either empty or it contains a point which is fixed with respect to
is either empty or it contains a point which is fixed with respect to 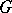 . Hence the generalization of the theorem of conjugation of Borel subgroup is: If the field
. Hence the generalization of the theorem of conjugation of Borel subgroup is: If the field 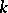 is perfect, the maximal connected solvable
is perfect, the maximal connected solvable 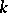 -split subgroups of a connected
-split subgroups of a connected 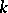 -defined algebraic group
-defined algebraic group 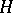 are mutually conjugate by elements of the group of
are mutually conjugate by elements of the group of 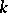 -points of
-points of 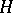 [2].
[2].
References
| [1] | A. Borel, "Groupes linéaires algébriques" Ann. of Math. (2) , 64 : 1 (1956) pp. 20–82 |
| [2] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [3] | V.V. Morozov, Dokl. Akad. Nauk SSSR , 36 : 3 (1942) pp. 91–94 |
Borel fixed-point theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel_fixed-point_theorem&oldid=18267