Difference between revisions of "Borel-Cantelli lemma"
m (TeX) |
|||
| Line 9: | Line 9: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017040/b0170406.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017040/b0170406.png" /></td> </tr></table> | ||
| − | If the events | + | If the events $A_n$ are mutually independent, then $\mathbb{P}(A) = 1$ or $0$, depending on whether the series <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017040/b0170409.png" /> converges or diverges, i.e. in this case the condition (*) is necessary and sufficient for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017040/b01704010.png" />; this is the so-called Borel criterion for "zero or one" (cf. [[Zero-one law|Zero-one law]]). This last criterion can be generalized to include certain classes of dependent events. The Borel–Cantelli lemma is used, for example, to prove the [[Strong law of large numbers|strong law of large numbers]]. |
====References==== | ====References==== | ||
Revision as of 09:42, 8 October 2014
2020 Mathematics Subject Classification: Primary: 60-01 Secondary: 60F1560F20 [MSN][ZBL]
A frequently used statement on infinite sequences of random events. Let $A_1,\dots, A_n, \dots$ be a sequence of events from a certain probability space and let $A$ be the event consisting in the occurance of (only) a finite number out of the events $A_n$, $n=1,2\dots$. Then, according to the Borel–Cantelli lemma, if
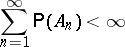 | (*) |
then
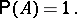 |
If the events $A_n$ are mutually independent, then $\mathbb{P}(A) = 1$ or $0$, depending on whether the series 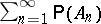 converges or diverges, i.e. in this case the condition (*) is necessary and sufficient for
converges or diverges, i.e. in this case the condition (*) is necessary and sufficient for 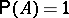 ; this is the so-called Borel criterion for "zero or one" (cf. Zero-one law). This last criterion can be generalized to include certain classes of dependent events. The Borel–Cantelli lemma is used, for example, to prove the strong law of large numbers.
; this is the so-called Borel criterion for "zero or one" (cf. Zero-one law). This last criterion can be generalized to include certain classes of dependent events. The Borel–Cantelli lemma is used, for example, to prove the strong law of large numbers.
References
| [B] | E. Borel, "Les probabilités dénombrables et leurs applications arithmetiques" Rend. Circ. Mat. Palermo (2) , 27 (1909) pp. 247–271 Zbl 40.0283.01 |
| [C] | F.P. Cantelli, "Sulla probabilità come limite della frequenza" Atti Accad. Naz. Lincei , 26 : 1 (1917) pp. 39–45 Zbl 46.0779.02 |
| [L] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) MR0203748 Zbl 0108.14202 |
Comments
The Borel–Cantelli lemma can be used in number theory to prove the so-called "normality" of almost-all natural numbers, cf. [F], Chapt. 8, Sect. 6.
References
| [F] | W. Feller, "An introduction to probability theory and its applications", 1 , Wiley (1957) pp. Chapt.14 |
Borel-Cantelli lemma. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel-Cantelli_lemma&oldid=33512