Boolean ring

An associative ring whose elements are all idempotent, i.e. for any . Any Boolean ring is commutative and is a subdirect sum of fields of two elements, and for all . A finite Boolean ring is a direct sum of fields and therefore has a unit element.

A Boolean ring is the ring version of a Boolean algebra, namely: Any Boolean algebra is a Boolean ring with a unit element under the operations of addition and multiplication defined by the rules

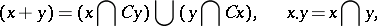where is the complement of . The zero and the unit of the ring are the same as, respectively, the zero and the unit of the algebra. Conversely, every Boolean ring with a unit element is a Boolean algebra under the operations , , .

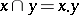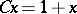References

[1]	M.H. Stone, "The theory of representations for Boolean algebras" Trans. Amer. Math. Soc. , 40 (1936) pp. 37–111
[2]	I.I. Zhegalkin, "On the technique of computation of propositions in symbolic logic" Mat. Sb. , 34 : 1 (1927) pp. 9–28 (In Russian) (French abstract)
[3]	D.A. Vladimirov, "Boolesche Algebren" , Akademie Verlag (1978) (Translated from Russian)
[4]	R. Sikorski, "Boolean algebras" , Springer (1969)

Comments

The operation is known as the symmetric difference. Think of the Boolean algebra of all subsets of a given set under union, intersection and complement to interpret these formulas.

References

[a1]	S. Rudeanu, "Boolean functions and equations" , North-Holland (1974)