Difference between revisions of "Boolean functions, normal forms of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | Formulas of a special kind realizing Boolean functions. One distinguishes between disjunctive normal forms (cf. [[Boolean functions, minimization of|Boolean functions, minimization of]]) and conjunctive normal forms. A product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169701.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169702.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169703.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169704.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169705.png" />, is called an elementary conjunction of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169706.png" /> if all its variables are different; | + | Formulas of a special kind realizing Boolean functions. One distinguishes between disjunctive normal forms (cf. [[Boolean functions, minimization of|Boolean functions, minimization of]]) and conjunctive normal forms. A product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169701.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169702.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169703.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169704.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169705.png" />, is called an elementary conjunction of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169706.png" /> if all its variables are different; "1" is considered to be an elementary conjunction of rank zero. A logical sum <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169707.png" /> is called an elementary disjunction of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169708.png" /> if all its variables are different; "0" is considered to be an elementary disjunction of rank zero. |
A formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169709.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697010.png" /> are distinct elementary conjunctions of ranks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697011.png" />, respectively, is called a disjunctive normal form, and the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697012.png" /> is called its complexity; a formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697013.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697014.png" /> are different elementary disjunctions of ranks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697015.png" />, respectively, is called a conjunctive normal form, and the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697016.png" /> is called its complexity. Every Boolean function that does not vanish identically can be defined by a disjunctive normal form which is, generally speaking, not unique. The same applies to conjunctive normal forms and functions that do not identically vanish. | A formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b0169709.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697010.png" /> are distinct elementary conjunctions of ranks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697011.png" />, respectively, is called a disjunctive normal form, and the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697012.png" /> is called its complexity; a formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697013.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697014.png" /> are different elementary disjunctions of ranks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697015.png" />, respectively, is called a conjunctive normal form, and the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697016.png" /> is called its complexity. Every Boolean function that does not vanish identically can be defined by a disjunctive normal form which is, generally speaking, not unique. The same applies to conjunctive normal forms and functions that do not identically vanish. | ||
| Line 5: | Line 5: | ||
From a table defining a Boolean function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697017.png" /> one easily obtains the perfect disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697020.png" />, and the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697021.png" /> are such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697022.png" />. The perfect disjunctive normal form realizing a Boolean function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697023.png" /> is unique. The perfect conjunctive normal form is defined similarly. | From a table defining a Boolean function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697017.png" /> one easily obtains the perfect disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697018.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697020.png" />, and the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697021.png" /> are such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697022.png" />. The perfect disjunctive normal form realizing a Boolean function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697023.png" /> is unique. The perfect conjunctive normal form is defined similarly. | ||
| − | Since for | + | Since for "almost-all" Boolean functions the number of unit sets varies between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697025.png" />, the asymptotic complexity of the perfect disjunctive normal form for "almost-all" Boolean functions is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697026.png" />. The maximal complexity of the perfect disjunctive normal forms for functions in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697027.png" /> variables is attained for functions that vanish at a single point. This complexity is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697028.png" />. |
The main problem in the theory of normal forms of Boolean functions is that of minimizing Boolean functions, i.e. the construction of conjunctive or disjunctive normal forms of minimal complexity — minimal conjunctive or disjunctive normal forms for any given Boolean function (cf. [[Boolean functions, minimization of|Boolean functions, minimization of]]; [[Algorithm, local|Algorithm, local]]). Here, by virtue of the duality principle, it is sufficient to consider disjunctive normal forms only. In connection with the problem of minimizing Boolean functions one also considers abridged dead-end, shortest and minimal disjunctive normal forms. An important problem in the theory of disjunctive normal forms is the search for numerical characteristics of them, and characteristics connecting various types of disjunctive normal forms of a given function. | The main problem in the theory of normal forms of Boolean functions is that of minimizing Boolean functions, i.e. the construction of conjunctive or disjunctive normal forms of minimal complexity — minimal conjunctive or disjunctive normal forms for any given Boolean function (cf. [[Boolean functions, minimization of|Boolean functions, minimization of]]; [[Algorithm, local|Algorithm, local]]). Here, by virtue of the duality principle, it is sufficient to consider disjunctive normal forms only. In connection with the problem of minimizing Boolean functions one also considers abridged dead-end, shortest and minimal disjunctive normal forms. An important problem in the theory of disjunctive normal forms is the search for numerical characteristics of them, and characteristics connecting various types of disjunctive normal forms of a given function. | ||
| − | The abridged disjunctive normal form is uniquely constructed from a Boolean function by means of a fairly simple algorithm. Its most important property is the fact that every minimal disjunctive normal form of a function and at least one shortest form can be obtained from the abridged disjunctive normal form by the elimination of certain elementary conjunctions. Therefore many minimization algorithms employ the abridged disjunctive normal form as the initial specification of a Boolean function. It is of major interest in this context to define the complexity of abridged disjunctive normal forms for | + | The abridged disjunctive normal form is uniquely constructed from a Boolean function by means of a fairly simple algorithm. Its most important property is the fact that every minimal disjunctive normal form of a function and at least one shortest form can be obtained from the abridged disjunctive normal form by the elimination of certain elementary conjunctions. Therefore many minimization algorithms employ the abridged disjunctive normal form as the initial specification of a Boolean function. It is of major interest in this context to define the complexity of abridged disjunctive normal forms for "almost-all" functions and to determine the absolute maximum of this complexity. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697029.png" /> is the number of elementary conjunctions in the abridged disjunctive normal form of a Boolean function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697030.png" /> and if |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697031.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697031.png" /></td> </tr></table> | ||
| Line 17: | Line 17: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697032.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697032.png" /></td> </tr></table> | ||
| − | and for | + | and for "almost-all" Boolean functions |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697033.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697033.png" /></td> </tr></table> | ||
| Line 23: | Line 23: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697034.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697034.png" /></td> </tr></table> | ||
| − | It is clear from these results and from the estimates of the complexity of the perfect disjunctive normal form that the complexity of the abridged disjunctive normal form is much higher than that of the perfect disjunctive normal form, both in the | + | It is clear from these results and from the estimates of the complexity of the perfect disjunctive normal form that the complexity of the abridged disjunctive normal form is much higher than that of the perfect disjunctive normal form, both in the "typical" and in the "record-breaking" cases. Unlike the perfect and the abridged disjunctive normal form, a given Boolean function may have many dead-end and minimal disjunctive normal forms. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697035.png" /> be the number of dead-end disjunctive normal forms and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697036.png" /> be the number of minimal disjunctive normal forms of a Boolean function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697037.png" />, |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697038.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697038.png" /></td> </tr></table> | ||
| Line 31: | Line 31: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697039.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697039.png" /></td> </tr></table> | ||
| − | and for | + | and for "almost-all" Boolean functions |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697040.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697040.png" /></td> </tr></table> | ||
| Line 39: | Line 39: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697042.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697042.png" /></td> </tr></table> | ||
| − | A non-trivial upper estimate for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697043.png" /> and a non-trivial estimate for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697044.png" /> for | + | A non-trivial upper estimate for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697043.png" /> and a non-trivial estimate for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697044.png" /> for "almost-all" functions are as yet (1977) not known. Complexity estimates of dead-end and of minimal disjunctive normal forms are of great interest in problems of minimization of Boolean functions. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697045.png" /> be the number of elementary conjunctions in a dead-end disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697046.png" /> of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697047.png" />; let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697048.png" /> be the number of elementary conjunctions in a shortest disjunctive normal form of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697049.png" />, |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697050.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697050.png" /></td> </tr></table> | ||
| Line 47: | Line 47: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697051.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697051.png" /></td> </tr></table> | ||
| − | For | + | For "almost-all" Boolean functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697052.png" /> and for almost-all dead-end disjunctive normal forms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697053.png" />: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697054.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697054.png" /></td> </tr></table> | ||
| − | For | + | For "almost-all" Boolean functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697055.png" />: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697056.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697056.png" /></td> </tr></table> | ||
| − | These estimates show that the shortest (and also the minimal) disjunctive normal forms of | + | These estimates show that the shortest (and also the minimal) disjunctive normal forms of "almost-all" Boolean functions account for only a small fraction of the number of dead-end disjunctive normal forms. There are also estimates of the relative complexity of dead-end and shortest disjunctive normal forms of Boolean functions. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697057.png" /> be the maximal number of elementary conjunctions in a dead-end disjunctive normal form of a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697058.png" />. For "almost-all" Boolean functions |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697059.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697059.png" /></td> </tr></table> | ||
| Line 63: | Line 63: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697066.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697066.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697067.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697068.png" /> are arbitrary dead-end disjunctive normal forms realizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697069.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697070.png" /> is the number of characters in the dead-end disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697071.png" />. Examples of Boolean functions with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697072.png" /> have been constructed; it has been established, however, that for | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697067.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697068.png" /> are arbitrary dead-end disjunctive normal forms realizing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697069.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697070.png" /> is the number of characters in the dead-end disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697071.png" />. Examples of Boolean functions with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697072.png" /> have been constructed; it has been established, however, that for "almost-all" Boolean functions |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697073.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016970/b01697073.png" /></td> </tr></table> | ||
| Line 70: | Line 70: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Yu.L. Vasil'ev, "On comparing the complexity of typical and disjunctive normal forms" ''Problemy Kibernet.'' : 10 (1963) pp. 5–61 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Glagolev, "Certain estimates of the disjunctive normal forms of functions of the algebra of logic" ''Problemy Kibernet.'' , '''19''' (1967) pp. 75–94 (In Russian) {{MR|225634}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.D. Korshunov, "The upper complexity bound of the shortest disjunctive normal forms of almost all Boolean functions" ''Cybernetics'' , '''5''' : 6 (1969) pp. 705–715 ''Kibernetika (Kiev)'' : 6 (1969) pp. 1–8</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.A. Sapozhenko, "On the greatest length of a dead-end disjunctive normal form for almost all Boolean functions" ''Math. Notes'' , '''4''' : 6 (1968) pp. 881 ''Mat. Zametki'' , '''4''' : 6 (1968) pp. 649–658 {{MR|}} {{ZBL|0177.02001}} </TD></TR></table> |
Revision as of 16:55, 15 April 2012
Formulas of a special kind realizing Boolean functions. One distinguishes between disjunctive normal forms (cf. Boolean functions, minimization of) and conjunctive normal forms. A product 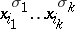 , where
, where 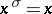 if
if 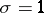 and
and  if
if 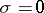 , is called an elementary conjunction of rank
, is called an elementary conjunction of rank 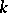 if all its variables are different; "1" is considered to be an elementary conjunction of rank zero. A logical sum
if all its variables are different; "1" is considered to be an elementary conjunction of rank zero. A logical sum 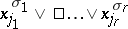 is called an elementary disjunction of rank
is called an elementary disjunction of rank  if all its variables are different; "0" is considered to be an elementary disjunction of rank zero.
if all its variables are different; "0" is considered to be an elementary disjunction of rank zero.
A formula 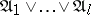 , where
, where 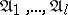 are distinct elementary conjunctions of ranks
are distinct elementary conjunctions of ranks  , respectively, is called a disjunctive normal form, and the number
, respectively, is called a disjunctive normal form, and the number 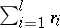 is called its complexity; a formula
is called its complexity; a formula 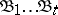 , where
, where 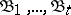 are different elementary disjunctions of ranks
are different elementary disjunctions of ranks 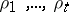 , respectively, is called a conjunctive normal form, and the number
, respectively, is called a conjunctive normal form, and the number 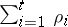 is called its complexity. Every Boolean function that does not vanish identically can be defined by a disjunctive normal form which is, generally speaking, not unique. The same applies to conjunctive normal forms and functions that do not identically vanish.
is called its complexity. Every Boolean function that does not vanish identically can be defined by a disjunctive normal form which is, generally speaking, not unique. The same applies to conjunctive normal forms and functions that do not identically vanish.
From a table defining a Boolean function 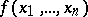 one easily obtains the perfect disjunctive normal form
one easily obtains the perfect disjunctive normal form 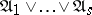 , where
, where 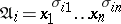 ,
, 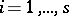 , and the sets
, and the sets  are such that
are such that 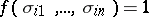 . The perfect disjunctive normal form realizing a Boolean function
. The perfect disjunctive normal form realizing a Boolean function 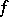 is unique. The perfect conjunctive normal form is defined similarly.
is unique. The perfect conjunctive normal form is defined similarly.
Since for "almost-all" Boolean functions the number of unit sets varies between 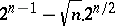 and
and 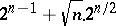 , the asymptotic complexity of the perfect disjunctive normal form for "almost-all" Boolean functions is
, the asymptotic complexity of the perfect disjunctive normal form for "almost-all" Boolean functions is  . The maximal complexity of the perfect disjunctive normal forms for functions in
. The maximal complexity of the perfect disjunctive normal forms for functions in  variables is attained for functions that vanish at a single point. This complexity is
variables is attained for functions that vanish at a single point. This complexity is  .
.
The main problem in the theory of normal forms of Boolean functions is that of minimizing Boolean functions, i.e. the construction of conjunctive or disjunctive normal forms of minimal complexity — minimal conjunctive or disjunctive normal forms for any given Boolean function (cf. Boolean functions, minimization of; Algorithm, local). Here, by virtue of the duality principle, it is sufficient to consider disjunctive normal forms only. In connection with the problem of minimizing Boolean functions one also considers abridged dead-end, shortest and minimal disjunctive normal forms. An important problem in the theory of disjunctive normal forms is the search for numerical characteristics of them, and characteristics connecting various types of disjunctive normal forms of a given function.
The abridged disjunctive normal form is uniquely constructed from a Boolean function by means of a fairly simple algorithm. Its most important property is the fact that every minimal disjunctive normal form of a function and at least one shortest form can be obtained from the abridged disjunctive normal form by the elimination of certain elementary conjunctions. Therefore many minimization algorithms employ the abridged disjunctive normal form as the initial specification of a Boolean function. It is of major interest in this context to define the complexity of abridged disjunctive normal forms for "almost-all" functions and to determine the absolute maximum of this complexity. If 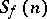 is the number of elementary conjunctions in the abridged disjunctive normal form of a Boolean function
is the number of elementary conjunctions in the abridged disjunctive normal form of a Boolean function 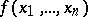 and if
and if
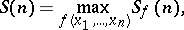 |
then the following estimates hold:
 |
and for "almost-all" Boolean functions
 |
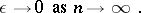 |
It is clear from these results and from the estimates of the complexity of the perfect disjunctive normal form that the complexity of the abridged disjunctive normal form is much higher than that of the perfect disjunctive normal form, both in the "typical" and in the "record-breaking" cases. Unlike the perfect and the abridged disjunctive normal form, a given Boolean function may have many dead-end and minimal disjunctive normal forms. Let 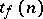 be the number of dead-end disjunctive normal forms and let
be the number of dead-end disjunctive normal forms and let 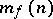 be the number of minimal disjunctive normal forms of a Boolean function
be the number of minimal disjunctive normal forms of a Boolean function 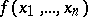 ,
,
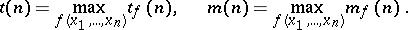 |
Then the following estimates hold:
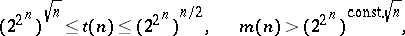 |
and for "almost-all" Boolean functions
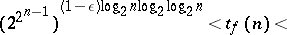 |
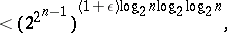 |
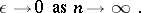 |
A non-trivial upper estimate for 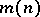 and a non-trivial estimate for
and a non-trivial estimate for 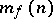 for "almost-all" functions are as yet (1977) not known. Complexity estimates of dead-end and of minimal disjunctive normal forms are of great interest in problems of minimization of Boolean functions. Let
for "almost-all" functions are as yet (1977) not known. Complexity estimates of dead-end and of minimal disjunctive normal forms are of great interest in problems of minimization of Boolean functions. Let  be the number of elementary conjunctions in a dead-end disjunctive normal form
be the number of elementary conjunctions in a dead-end disjunctive normal form 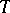 of the function
of the function  ; let
; let 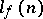 be the number of elementary conjunctions in a shortest disjunctive normal form of
be the number of elementary conjunctions in a shortest disjunctive normal form of 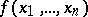 ,
,
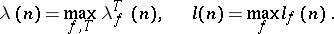 |
The following estimates then hold:
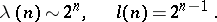 |
For "almost-all" Boolean functions 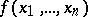 and for almost-all dead-end disjunctive normal forms
and for almost-all dead-end disjunctive normal forms 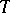 :
:
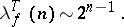 |
For "almost-all" Boolean functions 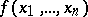 :
:
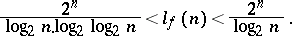 |
These estimates show that the shortest (and also the minimal) disjunctive normal forms of "almost-all" Boolean functions account for only a small fraction of the number of dead-end disjunctive normal forms. There are also estimates of the relative complexity of dead-end and shortest disjunctive normal forms of Boolean functions. Let 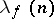 be the maximal number of elementary conjunctions in a dead-end disjunctive normal form of a function
be the maximal number of elementary conjunctions in a dead-end disjunctive normal form of a function 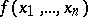 . For "almost-all" Boolean functions
. For "almost-all" Boolean functions
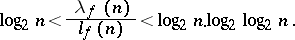 |
The maximum value of the ratio  can be estimated from below by
can be estimated from below by 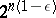 ,
, 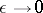 as
as 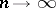 . Estimates of
. Estimates of 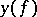 — the so-called scatter of
— the so-called scatter of 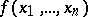 — have also been obtained. Here
— have also been obtained. Here
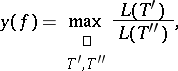 |
where 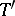 and
and 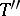 are arbitrary dead-end disjunctive normal forms realizing
are arbitrary dead-end disjunctive normal forms realizing 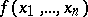 , and
, and 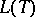 is the number of characters in the dead-end disjunctive normal form
is the number of characters in the dead-end disjunctive normal form  . Examples of Boolean functions with
. Examples of Boolean functions with 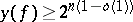 have been constructed; it has been established, however, that for "almost-all" Boolean functions
have been constructed; it has been established, however, that for "almost-all" Boolean functions
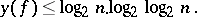 |
The estimates above give a fairly complete idea of the difficulties that arise when Boolean functions are minimized according to the scheme: perfect disjunctive normal form — abridged disjunctive normal form — dead-end disjunctive normal form — minimal disjunctive normal form.
References
| [1] | Yu.L. Vasil'ev, "On comparing the complexity of typical and disjunctive normal forms" Problemy Kibernet. : 10 (1963) pp. 5–61 (In Russian) |
| [2] | V.V. Glagolev, "Certain estimates of the disjunctive normal forms of functions of the algebra of logic" Problemy Kibernet. , 19 (1967) pp. 75–94 (In Russian) MR225634 |
| [3] | A.D. Korshunov, "The upper complexity bound of the shortest disjunctive normal forms of almost all Boolean functions" Cybernetics , 5 : 6 (1969) pp. 705–715 Kibernetika (Kiev) : 6 (1969) pp. 1–8 |
| [4] | A.A. Sapozhenko, "On the greatest length of a dead-end disjunctive normal form for almost all Boolean functions" Math. Notes , 4 : 6 (1968) pp. 881 Mat. Zametki , 4 : 6 (1968) pp. 649–658 Zbl 0177.02001 |
Boolean functions, normal forms of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boolean_functions,_normal_forms_of&oldid=16364