Boolean circuit
An  -ary Boolean function
-ary Boolean function  is a function from
is a function from 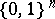 with values in
with values in 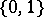 . The values
. The values  ,
, 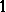 are called Boolean values, or bits, or truth values if they are identified with false and true (cf. also Boolean function). Elements of
are called Boolean values, or bits, or truth values if they are identified with false and true (cf. also Boolean function). Elements of 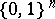 are Boolean strings of length
are Boolean strings of length  (or bit strings).
(or bit strings). 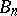 is the set of all
is the set of all 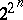
 -ary Boolean functions.
-ary Boolean functions.
A basis of connectives is any non-empty set  of Boolean functions, not necessarily of the same arity. An
of Boolean functions, not necessarily of the same arity. An  -formula for
-formula for 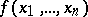 is a formula built from Boolean variables
is a formula built from Boolean variables  using connectives from
using connectives from  . A basis
. A basis  is complete if all Boolean functions are definable by an
is complete if all Boolean functions are definable by an  -formula. Examples of complete bases are:
-formula. Examples of complete bases are: 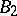 , the set of all binary Boolean functions, or the DeMorgan basis
, the set of all binary Boolean functions, or the DeMorgan basis 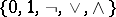 .
.
A more general way to define (equivalently, compute) Boolean functions is by circuits (straight line programs) that are simplified mathematical models of integrated circuits. A Boolean circuit over a basis  for
for 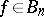 is a sequence
is a sequence 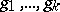 of functions from
of functions from 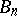 such that
such that 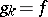 and such that any
and such that any 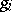 is either one of the projections
is either one of the projections  or is equal to
or is equal to 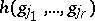 , for some
, for some 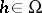 and
and 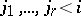 . Drawing directed edges from all such
. Drawing directed edges from all such  to
to 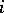 , and labelling
, and labelling 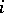 by
by 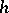 , defines a labelled directed acyclic graph (cf. also Graph, oriented). The size of the circuit is
, defines a labelled directed acyclic graph (cf. also Graph, oriented). The size of the circuit is 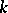 . The maximum length of a path from a vertex corresponding to one of the inputs
. The maximum length of a path from a vertex corresponding to one of the inputs  to
to 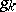 is the depth of the circuit. Note that formulas are circuits whose graphs are trees.
is the depth of the circuit. Note that formulas are circuits whose graphs are trees.
There are three basic ways to measure the complexity of a Boolean function, given a basis  :
:
the minimum size 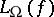 of an
of an  -formula defining
-formula defining 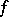 ,
,
the minimum size 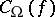 of a circuit over
of a circuit over  defining
defining 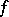 , and
, and
the minimum depth 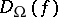 of a circuit over
of a circuit over  defining
defining 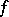 . For two complete bases
. For two complete bases  ,
, 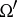 , the measures
, the measures 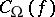 ,
, 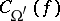 and
and 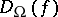 ,
, 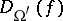 are proportional to each other, and
are proportional to each other, and 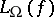 ,
, 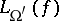 are polynomially related. A relation exists between the formula size and the circuit depth (see [a13]):
are polynomially related. A relation exists between the formula size and the circuit depth (see [a13]): 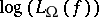 and
and 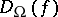 are proportional to each other, provided
are proportional to each other, provided  is finite.
is finite.
By estimating the number of circuits of a bounded size, C.E. Shannon [a11] proved (cf. [a14] for an optimal computation) that for almost-all 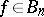 ,
, 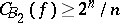 . On the other hand,
. On the other hand,
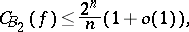 |
for all 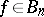 , see [a8].
, see [a8].
For a formal language 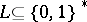 , let
, let 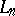 be the characteristic function of
be the characteristic function of 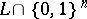 . The main open problem in Boolean complexity theory (cf. [a4]) is whether there is a language
. The main open problem in Boolean complexity theory (cf. [a4]) is whether there is a language 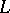 accepted by a non-deterministic polynomial-time Turing machine (cf. also Turing machine) such that
accepted by a non-deterministic polynomial-time Turing machine (cf. also Turing machine) such that 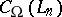 is not bounded by any polynomial in
is not bounded by any polynomial in  . The importance of this question stems from the fact that the affirmative answer implies that the computational complexity classes
. The importance of this question stems from the fact that the affirmative answer implies that the computational complexity classes 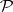 and
and 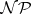 are different, as
are different, as 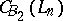 is bounded by a polynomial for any
is bounded by a polynomial for any 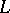 decidable in polynomial time (cf. [a10] and also
decidable in polynomial time (cf. [a10] and also 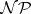 ).
).
No super-linear lower bounds on 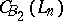 are known for any
are known for any 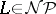 . However, if additional restrictions are put on the circuits, then strong lower bounds are known. Most notable are two results: any circuit of depth
. However, if additional restrictions are put on the circuits, then strong lower bounds are known. Most notable are two results: any circuit of depth 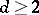 over a DeMorgan-like basis
over a DeMorgan-like basis  , allowing
, allowing 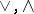 of unbounded arity, computing the parity function
of unbounded arity, computing the parity function 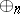 must have size at least
must have size at least 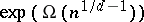 (see [a1], [a5], [a15], [a6]), and any circuit in the monotone basis
(see [a1], [a5], [a15], [a6]), and any circuit in the monotone basis 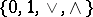 computing whether or not a graph on
computing whether or not a graph on  vertices contains a clique of size at least
vertices contains a clique of size at least 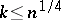 must have size at least
must have size at least  (see [a9], [a3]).
(see [a9], [a3]).
Interesting upper bounds are also known: a DeMorgan circuit of size 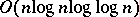 for multiplication of two
for multiplication of two  -bit long numbers, [a12] (it is still open (1998) if there are linear size circuits), and a monotone DeMorgan sorting network of simultaneous size
-bit long numbers, [a12] (it is still open (1998) if there are linear size circuits), and a monotone DeMorgan sorting network of simultaneous size 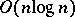 and depth
and depth  , see [a2].
, see [a2].
Various parts of computational complexity (cf. also Complexity theory) are directly related to lower-bound problems for Boolean functions; for example, communication complexity, cf. [a7].
References
| [a1] | M. Ajtai, "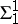 - formulae on finite structures" Ann. Pure Appl. Logic , 24 (1983) pp. 1–48 - formulae on finite structures" Ann. Pure Appl. Logic , 24 (1983) pp. 1–48 |
| [a2] | M. Ajtai, J. Komlós, E. Szemerédi, "An 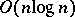 sorting network" Combinatorica , 3 (1983) pp. 1–19 sorting network" Combinatorica , 3 (1983) pp. 1–19 |
| [a3] | N. Alon, R. Boppana, "The monotone circuit complexity of Boolean functions" Combinatorica , 7 : 1 (1987) pp. 1–22 |
| [a4] | R. Boppana, M. Sipser, "Complexity of finite functions" J. van Leeuwen (ed.) , Handbook of Theoretical Computer Science , A (1990) pp. 758–804; Chap.14 |
| [a5] | M. Furst, J.B. Saxe, M. Sipser, "Parity, circuits and the polynomial-time hierarchy" Math. Systems Theory , 17 (1984) pp. 13–27 |
| [a6] | J. Hastad, "Almost optimal lower bounds for small depth circuits" S. Micali (ed.) , Randomness and Computation , Adv. Comput. Res. , 5 , JAI Press (1989) pp. 143–170 |
| [a7] | E. Kushilevitz, N. Nisan, "Communication complexity" , Cambridge Univ. Press (1996) |
| [a8] | O.B. Lupanov, "A method of circuit synthesis" Izv. V.U.Z. (Radiofizika) , 1 : 1 (1958) pp. 120–140 (In Russian) |
| [a9] | A.A. Razborov, "Lower bounds on the monotone complexity of some Boolean functions" Soviet Math. Dokl. , 31 (1985) pp. 354–357 |
| [a10] | J.E. Savage, "Computational work and time on finite machines" J. ACM , 19 : 4 (1972) pp. 660–674 |
| [a11] | C.E. Shannon, "The synthesis of two-terminal switching circuits" Bell Systems Techn. J. , 28 : 1 (1949) pp. 59–98 |
| [a12] | A. Schonhage, V. Strassen, "Schnelle Multiplikation grosser Zahlen" Computing , 7 (1971) pp. 281–292 |
| [a13] | P.M. Spira, "On time-hardware complexity of tradeoffs for Boolean functions" , Proc. 4th Hawaii Symp. System Sciences , North Hollywood&Western Periodicals (1971) pp. 525–527 |
| [a14] | I. Wegener, "The complexity of Boolean functions" , Wiley&Teubner (1987) |
| [a15] | Y. Yao, "Separating the polynomial-time hierarchy by oracles" , Proc. 26th Ann. IEEE Symp. Found. Comput. Sci. (1985) pp. 1–10 |
Boolean circuit. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boolean_circuit&oldid=11501