Bonnet theorem
Bonnet's theorem on the existence and the uniqueness of a surface with given first and second fundamental forms . Let the following two quadratic forms be given:
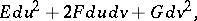 |
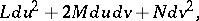 |
the first one of which is positive definite, and let the coefficients of these forms satisfy the Gauss equations (cf. Gauss theorem) and the Peterson–Codazzi equations. Then there exists a surface, which is unique up to motions in space, for which these forms are, respectively, the first and the second fundamental forms.
Bonnet's theorem on the diameter of an oval surface: If the curvature of an oval surface is larger than or equal to  at all its points, then the external diameter of this surface is smaller than
at all its points, then the external diameter of this surface is smaller than  ; this estimate cannot be improved. Stated by O. Bonnet in 1855.
; this estimate cannot be improved. Stated by O. Bonnet in 1855.
Comments
A proof of this theorem of Bonnet may be found in [a1] or [a2]. The Peterson–Codazzi equations are usually called the Mainardi–Codazzi equations, cf. [a1], after G. Mainardi (1857) and D. Codazzi (1868), who established them.
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
| [a2] | M. do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) |
Bonnet's theorem on the mean value, second mean-value theorem [2]: Let  be integrable functions on a segment
be integrable functions on a segment  and let
and let  be a positive decreasing function of
be a positive decreasing function of  ; then there exists a number
; then there exists a number  in
in  for which the equality
for which the equality
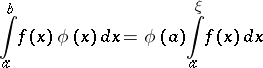 |
is valid. If 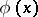 is merely required to be monotone, Bonnet's theorem states that there exists a point
is merely required to be monotone, Bonnet's theorem states that there exists a point  in
in  such that
such that
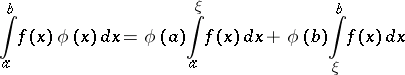 |
is true.
References
| [1a] | O. Bonnet, J. École Polytechnique , 24 (1865) pp. 204–230 |
| [1b] | O. Bonnet, J. École Polytechnique , 25 (1867) pp. 1–151 |
| [2] | O. Bonnet, "Rémarques sur quelques intégrales définies" J. Math. Pures Appl. , 14 (1849) pp. 249–256 |
T.Yu. Popova
Comments
Bonnet's original article is [a1].
References
| [a1] | O. Bonnet, C.R. Acad. Sci. Paris , 40 (1855) pp. 1311–1313 |
Bonnet theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bonnet_theorem&oldid=18094