Bonferroni inequalities
A solution of the classical matching problem and the counting inclusion-and-exclusion method (cf. also Inclusion-and-exclusion principle) can be given in a unified manner by the following set of inequalities. Let  be events on a given probability space, and let
be events on a given probability space, and let  denote the number of
denote the number of  that occur. Set
that occur. Set  and
and
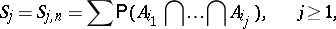 | (a1) |
where summation is over all subscripts  . The numbers
. The numbers  ,
,  , are known as the binomial moments of
, are known as the binomial moments of  , since, by turning to indicators, one immediately obtains that, with the expectation operator
, since, by turning to indicators, one immediately obtains that, with the expectation operator  ,
,
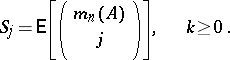 |
Now, the following inequalities are valid for all integers  and
and 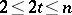 :
:
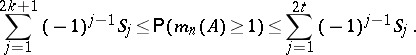 | (a2) |
Inequality (a2) can be rewritten for 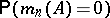 in the light of the elementary relation
in the light of the elementary relation 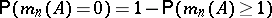 . Furthermore, it can be extended to
. Furthermore, it can be extended to
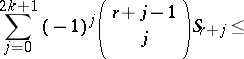 | (a3) |
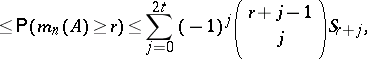 |
and
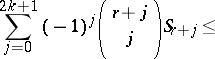 | (a4) |
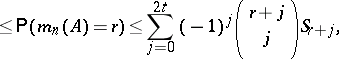 |
where  is an arbitrary integer with
is an arbitrary integer with 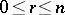 and the limits
and the limits 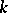 and
and 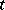 satisfy
satisfy 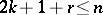 and
and 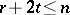 .
.
Inequalities (a2), (a3) and (a4) are known as the Bonferroni inequalities because of their extensive use by C.E. Bonferroni [a1] in statistical settings; this work of Bonferroni generated a considerable follow-up in later years. However, the inequalities above were known earlier: for discrete probability spaces they go back to the eighteenth century, whilst for an abstract, and thus general, probability space their validity appears in [a3].
When the probability 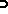 is just counting proportions (a very typical case in number theory), then (a2) is known as the method of inclusion-and-exclusion. However, each of (a2), (a3) or (a4) is a very useful tool with a generally underlying probability in such widely ranging topics as combinatorics, number theory, information theory, statistics, and extreme value theory. For detailed descriptions of all such applications, see [a2].
is just counting proportions (a very typical case in number theory), then (a2) is known as the method of inclusion-and-exclusion. However, each of (a2), (a3) or (a4) is a very useful tool with a generally underlying probability in such widely ranging topics as combinatorics, number theory, information theory, statistics, and extreme value theory. For detailed descriptions of all such applications, see [a2].
Although the Bonferroni inequalities are very effective tools in several problems, they may become impractical in others. In particular, when the general terms of 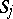 are known with an error term, then, because of the large number of terms in
are known with an error term, then, because of the large number of terms in 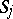 as a function of
as a function of  , the error terms might dominate the sum of the main terms in the Bonferroni bounds, making the results meaningless. Modifications of the Bonferroni inequalities, known as Bonferroni-type inequalities, overcome this difficulty.
, the error terms might dominate the sum of the main terms in the Bonferroni bounds, making the results meaningless. Modifications of the Bonferroni inequalities, known as Bonferroni-type inequalities, overcome this difficulty.
References
| [a1] | C.E. Bonferroni, "Teoria statistica delle classi e calcolo delle probabilità" Istit. Sup. Sci. Econ. Commerc. Firenze , 8 (1936) pp. 1–62 |
| [a2] | J. Galambos, I. Simonelli, "Bonferroni-type inequalities with applications" , Springer (1996) |
| [a3] | K. Jordan, "The foundations of the theory of probability" Mat. Phys. Lapok , 34 (1927) pp. 109–136 (In Hungarian) |
Bonferroni inequalities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bonferroni_inequalities&oldid=18515